对NP-hard问题，有几种处理方法：

• 为问题实例添加限制，相当于利用问题中的特殊结构简化问题
• 寻找精确算法
• 寻找近似算法

实例研究：

最大独立集(稳定集)问题：假设无向图G=(V(G),E(G))是无环的，求最大独立集 $I\subseteq V(G)$

若对于任意线性序列(linear ordering)，贪心算法都能找到最大独立集，则称此图是拟阵的(matroidal)

完美消除序列(Perfect Elimination Ordering)是一个 $V(G)$ 中的一个序列 $x_1,\cdots,x_n$ ，使得 $\forall 1\leq i\leq n$ ， $x_i$ 是 $G[\{x_i,\cdots,x_n\}]$ 中的简单点(simplicial vertex)。其中 $G[X]=(X,E(G)\cap X\times X)$ 是G的导出子图。

推论：任意区间图都有一个完美消除序列

定理：可以在多项式时间内得到区间图的一个区间表示，从这个区间表示可以得到一个完美消除序列

恰当染色(proper coloring)对应一个将顶点分为独立集的划分

色数(chromatic number)是最小的恰当染色的颜色数

定理：给定图G的一个完美消除序列，贪心染色算法使用的颜色数等于最大团的大小

分裂图(split graph)是可以划分成一个团和一个独立集的图

弦图(chordal graph)是没有一个长度大于4的环作为导出子图的图(顶点数大于3的环至少有一个弦)，弦图都是完美图

推论：每个分裂图都有完美消除序列。分裂图既是弦图，又是弦图的补图

定理：G有一个完美消除序列，当且仅当它是一个弦图

$S\subseteq V(G)$ 是一个分离子(separator)如果 $G[V(G)\setminus S]$ 有比G更多的连通分量

S是最小分离子，如果S是分离子且对任意 $x\in S$ ， $S\setminus x$ 不是分离子

引理：任意最小分离子都是一个团

图G的三角剖分是通过给G添加边得到的弦图

图的树宽(tree-width) $treewidth(G)=\{\omega(H)-1: H是G的最小三角剖分\}$ ，其中 $\omega(H)$ 是H的最大团的大小

最大团图(graph of maximal cliques)的顶点是最大团，相交的团之间有边且权重为交集大小

团树定理(clique tree theorem)：弦图的最小生成树是一个宽度为 $\omega(G)-1$ 的树分解(tree decomposition)

图G收缩(contracting)一个边xy后得到图 $G'=(V',E')$ ，$V'=V(G)\setminus \{x,y\}\cup \{z\}$ （z是新顶点）， $E'=E(G[V\setminus\{x,y\}])\cup \{zt: t\in N_G(x)\cup N_G(y)\}$ ($N_G(x)$ 是x的邻居顶点集)

H是G的一个子式(minor)如果H可以通过图G删除顶点，删除边或收缩边得到，子式的树宽小于等于原图的树宽

如果 $treewidth(G)=k$ 那么以G为主图(primal graph)的CSP问题可以在多项式时间内求解（使用k一致性算法）

将十六进制私钥转为WIF格式私钥并使用importprivkey导入bitcoin core

import hashlib
def str_cat(pk0):
    pk1 = '80' + pk0
    pk2 = hashlib.sha256(bytes.fromhex(pk1))
    pk3 = hashlib.sha256(pk2.digest())
    checksum = pk3.digest().hex()[0:8]
    address_hex = pk1 + str(checksum)
    return address_hex

def base58(address_hex):
    alphabet = '123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz'
    b58_string = ''
    # Get the number of leading zeros
    leading_zeros = len(address_hex) - len(address_hex.lstrip('0'))
    # Convert hex to decimal
    address_int = int(address_hex, 16)
    # Append digits to the start of string
    while address_int > 0:
        digit = address_int % 58
        digit_char = alphabet[digit]
        b58_string = digit_char + b58_string
        address_int //= 58
    # Add ‘1’ for each 2 leading zeros
    ones = leading_zeros // 2
    for one in range(ones):
        b58_string = '1' + b58_string
    return b58_string

def hex2WIF(pk):
    return base58(str_cat(pk))

bitcoin.conf示例

# reduce memory cost
dbcache=20
blocksonly=1
maxorphantx=10
maxmempool=100
maxsigcachesize=4
maxconnections=4
rpcthreads=1

# boost syncing
par=7
banscore=10
listen=0

1. 安装花生壳客户端

2. 启动

   sudo phddns enable

3. 登陆hsk.oray.com/console/manage/并在账号列表中添加SN码
4. 使用SN码和默认密码登陆http://b.oray.com并绑定账号，增加映射，使用相应模板，并填入对应内网IP，使用动态端口即可

指数加权平均(polyak averaging)：$\tau$是加权平均系数，它相当于一个超学习率，非常敏感，增大0.01就有可能会使训练发散。一般要保证$(1-\tau)^{n}$大约在10%左右，n是一个epoch的episodes数。总之要让Actor的Loss在100个epoch内爆炸到$(1-\gamma^T)/(1-\gamma)$的大小，其中$\gamma$是discount，T是一个episode最大时间步，Critic Loss也会跟着爆炸，之后它们会慢慢减小

Replay Buffer的大小可以小一点，几百个episodes就够了，这样可以防止记住错的reward

gamma的大小可以看着每个episode step的Q值来调，如果在出现reward前后变化得过快，则应调大gamma

batchsize应根据Critic Loss的不稳定性调，如果Critic Loss波动过于剧烈，则应调大batchsize，但不应引起训练速度过慢

旅馆预订问题

一个旅馆有k个房间，顾客的订单是三元组 $c_i=(t_i,a_i,d_i)$ ，其中 $t_i$ 是订单创建时间， $a_i$ 是入住时间， $d_i$ 是离开时间。此系统中包含三个实体(entity)：房东，房间，顾客。房间有空闲和被占两种状态。顾客有四种状态：被拒，接收，被分配房间 $r_j$ ，服务结束。房东可触发三种事件(event)：处理请求，接收/拒绝请求，分配房间 $r_j$ 给顾客 $c_i$ 。顾客可触发三种事件：创建订单，到达旅馆，离开旅馆。可能的活动(activity)为顾客 $c_i$ 住在房间 $r_j$ 。每天房东需要根据已经入住的情况和已经接收的订单来决定是否拒绝新订单。考虑三个表： $\sigma_t$ 为在第t天创建的订单列表， $\sigma_A$ 为接收但尚未到达的订单列表， $\sigma_S$ 为已经服务结束的订单列表。对于每个订单 $c_i\in \sigma_t$ ，房东需要使用一个算法来决定是否拒绝订单 $c_i$ ，试探性地分配 $r_i$ 房间给已接收的顾客。

FirstFit算法：

• 输入：房间总数k， $c_i=(a_i,r_i,d_i)\in\sigma_A,\sigma_S,c_i=(t,a_i,d_i)\in\sigma_t$
• 输出：接收/拒绝订单 $c_i$ ，为接收的订单 $c_i$ 分配房间 $r_i$

1. 以非递减的入住时间 $a_i$ 为 $\sigma_t$ 中的订单排序，若存在相等时间，则以非递减的离开时间 $d_i$ 排序。
2. 对 $c_i\in\sigma_t$ ，依次为 $c_i$ 分配在 $[a_i,d_i]$ 内未被占据的最小的房间号 $r_i$ 。若 $r_i\leq k$ 则接收 $c_i$ 并将其添加到 $\sigma_A$ 中，否则拒绝 $c_i$ 并从 $\sigma_t$ 中移除。

BestFit算法：

• 输入：房间总数k， $c_i=(a_i,r_i,d_i)\in\sigma_A,\sigma_S,c_i=(t,a_i,d_i)\in\sigma_t$
• 输出：接收/拒绝订单 $c_i$ ，为接收的订单 $c_i$ 分配房间 $r_i$

1. 以非递减的入住时间 $a_i$ 为 $\sigma_t$ 中的订单排序，若存在相等时间，则分为一组同时处理。
2. 对 $c_i\in\sigma_t$ ，依次为 $c_i$ 分配在 $[a_i,d_i]$ 内未被占据的刚好补上一个空的，或最小的房间号 $r_i$ 。若 $r_i\leq k$ 则接收 $c_i$ 并将其添加到 $\sigma_A$ 中，否则拒绝 $c_i$ 并从 $\sigma_t$ 中移除。

Mealy机

Mealy机是有限自动机的一个变种，它可以在状态转移时打印出字母。Mealy机是一个五元组 $M=(Q,\mathcal V,\Gamma,\delta,q_0)$ ，其中： $Q$ 是状态集， $\mathcal V$ 是输入字母集， $\Gamma$ 是输出字母集， $\delta$ 是转移函数 $\delta:Q\times\mathcal V\to Q\times \Gamma$ ， $q_0$ 是初始状态。在Mealy机中，转移函数是确定性的。

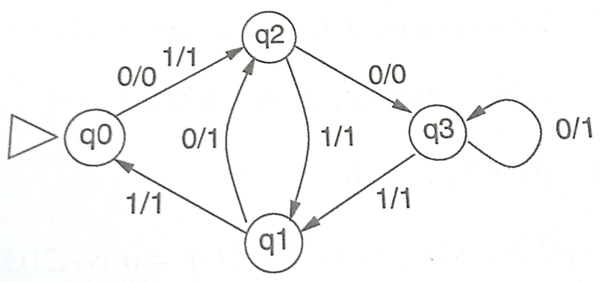
对一个序列反馈电路，状态 $q(t)=I(t) \vee B(t)$ ，新状态由旧状态和输入共同决定： $q(t+1)=(A(t+1),B(t+1))$ ， $A(t+1)=I(t) \barwedge (A(t)\vee B(t))$ ， $B(t+1)=A(t)$ ，对应的Mealy机图为：

向量加法系统(Vector addition systems, VAS)

一个VAS是一个有限集合 $U\subseteq \mathbb Z^d, d>0$ 。初始向量编码多个计数器的初始值，VAS中的向量表示更新。通常情况下，这些计数器的值不小于0。给定一个初始向量 $x^0\in \mathbb N^d$ ，向量 $u\in U$ 可以逐项与其做加法，只要保证中间向量 $x^t\in \mathbb N^d$ 。

例：一个系统有4个计数器，VAS $U$ 中有3个向量：

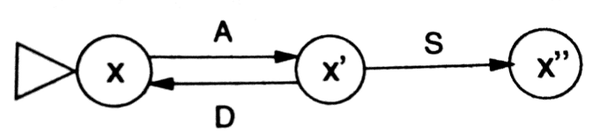
$A=\begin{pmatrix}-1\\-1\\1\\0\end{pmatrix},D=\begin{pmatrix}1\\1\\-1\\0\end{pmatrix},S=\begin{pmatrix}1\\0\\-1\\1\end{pmatrix}$

初始向量 $x=(1,1,0,0)^\top$ ，则有如下状态转换图

Petri网

Petri网是一个四元组 $(P,T,f,m_o)$ ，P是地点集，T是转换集， $f:(P\times T)\cup (T\times P)\to \mathbb N_o$ 是流关系，它定义了有向边集，边的权重是非负整数，初始标记是 $m_o:P\to\mathbb N_o$ 。它也是一个加权二分有向图 $G=(P\cup T,A,w)$ ，其中 $P\cup T$ 是节点集，边集 $A$ 包含所有的转换 $pt,tp\subseteq (P\times T)\cup (T\times P)$ ， $f(pt),f(tp)>0$ ，边的权重满足 $w(a)=f(a)$ 。

发射规则(F1)：

• 当 $m(p)\geq f(p,t),\forall p\in \bullet t$ （t之前的地点集）时，转换t在标记m下被激活，记作 $m\ [t>$ ，否则t不被激活。
• 一个被激活的转换t可以发射。
• 当t在m下发射后，一个新的标记m'到达了，记作 $m[t>m'$ ，且有 $m'(p)=m(p)-f(p,t)+f(t,p),\forall p\in P$ 。
• 发射过程不消耗时间

状态空间：

给定一个Petri网$(P,T,f,m_o)$，从初始标记 $m_o$ 可达的标记集合 $[m_o>$ 是它的状态空间

可达图(Reachability graph)：

一个Petri网$(P,T,f,m_o)$的可达图的节点表示从 $m_o$ 可达的标记，边表示导致状态变化的转换的发射

更强的Petri网

在一个Petri网$(P,T,f,m_o)$中，若一些地点有 $B\subseteq P$ 有有限的容量，容量由正整数向量 $\mathbf c\in \mathbb Z_+^B$ ，则将$(P,T,f,m_o,\mathbf c)$称为有容Petri网(cPN)。其中一个转换t在m下被激活，如果

• $\forall p\in \bullet t, m(p)-w(pt)\geq 0$
• $\forall p\in t\bullet \cap B, m(p)+w(pt)\leq c_p$

一个扩展Petri网(xPN) $(P,T,(A\cup A_R\cup A_I),w)$ 有三种边，有正常边 $A$ 和两种控制边：读边 $A_R\subset P\times T$ 和阻碍边 $A_I\subset P\times T$ 。在扩展Petri网中，除了F1发射规则要满足外还要满足：

• $\forall (p,t)\in A_R,m(p)\geq w(pt)$
• $\forall (p,t)\in A_I,m(p)<w(tp)$

一个优先Petri网(pPN)是一个Petri网 $(P,T,f,m_o)$ 加上 $T\times T$ 上的偏序 $\mathcal O$ ，在优先Petri网中，转换的发射被由 $\mathcal O$ 表示的优先级控制。对被激活的转换t，除了F1发射规则要满足外还要满足：

• 不存在转换 $t'\in T(m)$ 且在$\mathcal O$中 $t'>t$

独立系统(Independence system)：对一个有限基础集V，一个集族 $\mathcal V\subseteq 2^V$ 是一个独立系统如果 $\mathcal F$ 满足如下条件：

• $\emptyset\in \mathcal F$
• 若 $F'\subseteq F\in \mathcal F$ ，则$F'\in \mathcal F$

$(V,\mathcal F,c)$ 的最大化问题：对一个独立系统 $(V,\mathcal F)$ 和一个目标函数向量 $\mathbf c\in \mathbb K_+^V$ ，求

$\max \left\{ \mathbf c(F)=\sum_{v\in F} c_v: F\in \mathcal I \right\}$

最大匹配问题(MMP)：给定图 $G=(V,E)$ ，求使 $|M|$ 最大的匹配 $M\subseteq E$ ，或对 $\mathbf w\in \mathbb R^E$ ，使权重 $\mathbf w(M)=\sum_{e\in M} w_e$ 最大的匹配

最大匹配问题是一个独立系统： $\max \left\{ \mathbf w(M)=\sum_{e\in M} w_e: M\in \mathcal M\right\}$

最大匹配问题是一个ILP：

$\max \sum_{e\in E} w_e x_e\\ s.t.\ \sum_{e\in \delta(v)} x_e\leq 1, \forall v\in V\\ x_e\in \{0,1\}, \forall e\in E$

最大稳定集问题(MSSP)：给定图 $G=(V,E)$ ，求使 $|S|$ 最大的稳定集 $S\subseteq V$ ，或对 $\mathbf w\in \mathbb R^E$ ，使权重 $\mathbf w(S)=\sum_{v\in S} w_v$ 最大的稳定集

最大稳定集问题是一个独立系统： $\max \left\{ \mathbf w(S)=\sum_{v\in S} w_v: S\in \mathcal S\right\}$

最大稳定集问题是一个ILP：

$\max \sum_{v\in V} w_v x_v\\ s.t.\ x_u+x_v\leq 1, \forall uv\in E\\ x_v\in \{0,1\}, \forall v\in V$

最小集合划分问题(MSPP)：给定有限基础集V和可行集组成的集族 $\mathcal F\subseteq 2^V$ ，求使 $|\mathcal P|$ 最小的V的划分 $\mathcal P\subseteq \mathcal F$ ，它是一个NP-hard问题

最小集合划分问题是一个ILP：

$\min \sum_{F\in \mathcal F}x_F\\ s.t.\ \sum_{F\ni i}x_F=1, \forall i\in V\\ x_F\in \{0,1\}, \forall F\in \mathcal F$

装箱问题(BPP)：给定基础集 $V=\{1,\cdots,n\}$ ，其中每个货物有权重 $\mathbf a\in \mathbb R_+^n$ ，箱子容量均为 $b\in \mathbb R_+, b\geq a_i,\forall i\in V$ ，求装箱需要的最少箱子数

装箱问题是一个MSPP

节点染色问题(NCP)：给图G=(V,E)染色使相邻节点颜色不同，并使用最少颜色

节点染色问题是一个ILP：

$\min \sum_{S\in \mathcal S}x_S\\ s.t.\ \sum_{S\ni i}x_S=1, \forall i\in V\\ x_S\in \{0,1\}, \forall S\in \mathcal S$

最小集合覆盖问题(MSCP)：给定有限基础集V和可行集组成的集族 $\mathcal F\subseteq 2^V$ ，求使 $|\mathcal C|$ 最小的V的覆盖 $\mathcal C\subseteq \mathcal F$

最小集合覆盖问题是一个ILP：

$\min \sum_{F\in \mathcal F}x_F\\ s.t.\ \sum_{F\ni i}x_F\geq1, \forall i\in V\\ x_F\in \{0,1\}, \forall F\in \mathcal F$

最小截线问题(MTP)：对 $(V,\mathcal F)$ 求基数最小的截线(transversal)。如果 $F',F\in \mathcal F,F'\subset F$ 则对任意截线 $T$ 有$T\cap F'\subset F$ ，因此只需考虑clutter $(V,\mathcal F)$ ，其中没有元素包含在另一个内。

最小截线问题是一个NP-hard问题

clutter矩阵： $M(\mathcal F)$ 由 $F\in\mathcal F$的关联向量作为行向量，是一个0/1矩阵

最小截线问题是一个ILP：

$\min \mathbf 1^\top x\\ s.t.\ M(\mathcal F)x\geq\mathbf 1\\ x\in \{0,1\}^V$

clutter $(V,\mathcal F)$ 可定义一个独立系统 $(V,\mathcal I)$ ， $\mathcal I=\{I\subseteq V:|I\cap F|\leq |F|-1,\forall F\in \mathcal F\}$

反过来一个独立系统 $(V,\mathcal I)$ 的circuits的集族 $\mathcal F=\{F\subseteq V: F\nsubseteq I, \forall I\in \mathcal I, F最小\}$ 可以定义一个clutter $(V,\mathcal F)$

等价关系：对仿射变换 $y=1-x$

$\min \mathbf 1^\top y\\ s.t.\ M(\mathcal F)y\geq\mathbf 1\\ y\in \{0,1\}^V$

和

$|V|-\max\mathbf 1^\top x\\ s.t.\ (x^F)^\top x\leq |F|-1,\forall F\in \mathcal F\\ x\in \{0,1\}^V$

等价。

理想表达式(Ideal formulation)：一个整数线性规划 $\max c^\top x, Ax\leq b, x\in \mathbb Z^n$ 是一个优化问题的理想表达式如果 $P(A,b)=\{x\in\mathbb R_+^n:Ax\leq b\}=conv\{x\in \mathbb Z^n_+:Ax\leq b\}$ ，即 $P(A,b)$ 只有整数极点

全单模(Total unimodualrity)：一个矩阵 $A\in \mathbb Z^{m\times n}$ 是全单模的，如果它的任意方子阵的行列式值属于集合 $\{-1,0,1\}$

定理： $P(A,b)=\{x\in \mathbb R_+^n:Ax\leq b\},\forall b\in \mathbb Z^m$ 是整的，当且仅当A是全单模的

定理：任意有向图的关联矩阵是全单模的

定理：最大流问题对整数容量有整数最优解

定理：最小割问题对整数向量有整数最优解

多边形表达式(Polyhedral formulation)的最大匹配问题：给定G=(V,E)和权重 $w\in \mathbb R_+^E$ ，求 $\max w^\top x, x\in Match(G)$ ，其中 $Match(G)=conv\{x^M\in\{0,1\}^E:M\subseteq E\ matching\}$ 是一个匹配多面体(polytope)。由松弛化得到 度约束多面体(degree constraint polytope)$DegM(G)=\{x\in[0,1]^E :\sum_{e\in\delta(v)}x_e\leq 1,\forall v\in V\}$

定理：矩阵 $M\in \mathbb Z^{m\times n}$ 是全单模的当且仅当任意子集 $J\subset\{1,\cdots,m\}$ 对应的行有二分集 $J_A\cup J_B=J$ ，使得对任意列 $i\in\{1,\dots,n\}$ ，有 $\sum_{j\in J_A} m_{ji}-\sum_{j\in J_B} m_{ji}\in\{-1,0,1\}$

定理：Match(G)=DegM(G)当且仅当G是二分的

定理：对任意图G=(V,E)，匹配多面体Match(G)包含所有满足度约束和奇数集(odd set)约束的 $x\in \mathbb R_+^E$ ，其中

• 度约束： $x(\delta(v))=\sum_{e\in\delta(v)} x_e \leq 1, \forall v\in V$
• 奇数集约束： $x(E(V'))=\sum_{e\in E(V')} x_e\leq \frac{|V'|-1}{2}, \forall V'\in \mathcal O$ 其中 $\mathcal O=\{V'\subseteq V:|V'|\geq 3, odd\}$ 表示奇数大小的节点集族， $E(V')$ 表示端点在V'内的边

因此有松弛化后的最大匹配问题的ILP形式：

$\max \sum_{e\in E} w_e x_e\\ s.t.\ x(\delta(v))=\sum_{e\in\delta(v)} x_e \leq 1, \forall v\in V\\ x(E(V'))=\sum_{e\in E(V')} x_e\leq \frac{|V'|-1}{2}, \forall V'\in \mathcal O\\ x_e\geq 0, \forall e\in E$

结论：存在 $O(\sqrt{|V|}\cdot |E|)$ 的解决最大基数匹配问题的组合算法，和 $O(|V|^3)$ 的解决最大权重匹配问题的组合算法

多边形表达式(Polyhedral formulation)的最大稳定集问题：给定G=(V,E)和权重 $w\in \mathbb R_+^V$ ，求 $\max w^\top x, x\in STAB(G)$ ，其中 $STAB(G)=conv\{x^S\in\{0,1\}^V:S\subseteq V\ stable\}$ 是一个稳定集多面体(polytope)。由松弛化得到 边约束稳定集多面体(edge constraint stable set polytope)$ESTAB(G)=\{x\in[0,1]^V : x_u+x_v\leq 1,\forall uv\in E\}$

定理：矩阵 $M\in \mathbb Z^{m\times n}$ 是全单模的当且仅当任意子集 $I\subset\{1,\cdots,n\}$ 对应的列有二分集 $I_A\cup I_B=I$ ，使得对任意列 $j\in\{1,\dots,m\}$ ，有 $\sum_{i\in I_A} m_{ji}-\sum_{i\in I_B} m_{ji}\in\{-1,0,1\}$

定理：STAB(G)=ESTAB(G)当且仅当G是二分的

定理：一个团Q和一个稳定集S至多有一个公共点

因此有团约束： $x(Q)=\sum_{v\in Q} x_v\leq 1, \forall Q\subseteq V是团$

松弛化后得到团约束稳定集多面体 $QSTAB(G)=\{x\in[0,1]^V :\sum_{v\in Q} x_v\leq 1,\forall Q\subseteq V是团\}$

定理：用 $\omega(G)$ 表示最大团大小， $\chi(G)$ 表示最小染色数，有 $\omega(G)\leq\chi(G)$

完美图：G是完美图当且仅当对G的任意诱导子图 $G'\subseteq G$ 有 $\omega(G')=\chi(G')$

定理：STAB(G)=QSTAB(G)当且仅当G是完美图

定理：对任意完美图，最大稳定集问题可以在多项式时间解决

截线问题的表达式：覆盖多边形(covering polyhedron) $Cov_I(A)=conv\{x\in \{0,1\}^V:Ax\geq \mathbf 1\}$ ，松弛化 $Cov(A)=\{x\in \mathbb R_+^V:Ax\geq \mathbf 1\}$ 是无界的，但是所有极点都在 $[0,1]^V$ 中。

理想cluter：一个clutter $\mathcal C$ 和clutter矩阵 $A=M(\mathcal C)$ 是理想的，如果松弛化Cov(A)有整数极点。阻碍子(blocker) $b(\mathcal C)=(V,\mathcal T)$ 是有 $\mathcal C$ 的最小截线作为超边的clutter

定理：一个clutter $\mathcal C$ 是理想的当且仅当它的阻碍子 $b(\mathcal C)$ 是理想的。Cov(M(C))是理想的当且仅当Cov(M(b(C)))是理想的

定理：有向图D中(s,t)路径的clutter DP(D)是理想的。有向图D中(s,t)割的clutter b(DP(D))是理想的

令 $\mathcal H=(E,\mathcal F)$ 为一个clutter， $\mathcal F $ 中两两不交的集合族是一个packing(matching)。最大packing的基数 $v(\mathcal H)$ 是最小截线的 $\tau(\mathcal H)$ 的下界。当 $v(\mathcal H)=\tau(\mathcal H)$ 时称这个clutter packs，此时对应的线性规划有整数最优解

定理：每个二分图都packs

定理：任意图G=(V,E)中，两两不交(s,t)路径的个数等于最小(s,t)割中的边数。令 $\mathcal P$ 为G中(s,t)路径的集族，超图 $P(G)=(E,\mathcal P)$ packs。

MFMC性质：令 $\mathcal C=(V,\mathcal E)$ 为一个clutter， $A=M(\mathcal C)$ 。若两个等价的线性规划

$\max \mathbf 1^\top y\\ s.t. A^\top y\leq w\\ y\geq 0$ 和

$\min w^\top x\\ Ax\geq \mathbf 1\\ x\geq 0$

对任意 $w\in\mathbb Z_+^V$ 有整数最优解，则 $\mathcal C$ 有MFMC性质

推论：MFMC性质可导出 $\mathcal C$ 是理想的且packs

推论：DP(D)有MFMC性质，b(DP(D))有MFMC性质

综上所述，以下情形下我们可以多项式时间内解决ILP

1. 原来的ILP表达式是理想的，P(A,b)是整的
2. 原表达式不理想，但是松弛化的约束系统容易找到
3. 一般情况下原表达式不理想，但是特殊情形下一些组合性质被满足了

增强表达式的方法：Cutting planes，Branch & Bound

精确和启发式算法：在线算法都是启发式算法

主启发规则(primal heuristic)找到一个可行解I，对偶启发规则找到最优解的下界 $b\leq c(I_{opt})\leq c(I)$

最优间隙(optimality gap)： $c(I)/c(I_{opt})$

对偶间隙(duality gap)： $c(I)/b$

最小化问题的k近似算法找到一个可行解I满足 $c(I)\leq k\cdot c(I_{opt}), k\geq 1$

对一个最小化问题，一个在线算法ALG是c-竞争性的如果ALG对任意请求序列 $\sigma$ 找到一个可行解 $ALG(\sigma)$ 满足 $ALG(\sigma)\leq c\cdot OPT(\sigma), c\geq 1$ ，ALG的竞争性系数(competitive ratio)是保证ALG是c竞争性的所有c的下确界

定理 Olariu1991：当 $\mathcal G(\mathcal I)$ 的节点按左端点升序排序后，贪心算法找到一个区间图(interval graph) $\mathcal G(\mathcal I)$ 的 $\omega(\mathcal G(\mathcal I))$ -染色

定理：旅馆预订问题的在线贪心染色算法是T竞争性的，其中T是总天数

度量任务系统(Metric task system）：一个度量任务系统是一个二元组 $(M,T)$ ，其中 $M=(X,d)$ 是一个度量空间， $T=(\tau_1,\cdots,\tau_n)$ 是任务集合。一个任务 $\tau_i$ 是一个访问特定点 $x_i\in X$ 的请求，或从起点 $x_s\in X$ 到终点 $x_d\in X$ 运输物体的请求。服务器 $server(s)$ 要处理任务集，目标是最小化走过的距离。

TSP是NP-hard问题，有启发规则2-OPT augmentation

定理(Sahni&Gonzalez1976)：设 $H_A$ 为A在 $(K_n,w)$ 中找到的TSP圈。若存在一个多项式的TSP启发规则A和一个常数 $1\leq\alpha<\infty$ 使得对任意TSP实例，有 $w(H_A)\leq \alpha w(H_{opt})$ ，则P=NP

定理(Ausiello 1998)：不存在在线TSP问题的确定性在线算法可以使竞争性系数c<2

定理：在线算法IGNORE和REPLAN在一般度量空间中对在线TSP问题是5/2-竞争性的

定理：存在在线算法在一般度量空间中对在线TSP问题有c=2的竞争性系数

定理(Manasse, McGeoch and Sleator1998)：对任意度量空间，在线kSP的竞争性系数至少为k

定理(Bsaybes, Quilliot, Wagler2018)：出租车问题(紧时间窗口，服务器容量为1的DARP)可以在多项式时间解决

推论：不存在在线PDP(Pickup & delivery)问题的确定性在线算法可以在一般度量空间上使竞争性系数c<2

定理(Ascheuer, Krumke, Rambau1998)：在线算法IGNORE和REPLAN对服务器容量C=1的在线PDP问题是5/2-竞争性的

定理：存在在线算法对服务器容量C=1的在线PDP问题有c=2的竞争性系数

定理(Bsaybes, Quilliot, Wagler2018)：对在线出租车问题，不存在竞争性的在线算法

带重分配的最大接收(Max-Accept Relocation Problem)问题：

• 边a的权重 $w_a$ 即司机沿a移动的消耗，节点v的权重 $c_v$ 即车站的容量。 $x^t\in \mathbb Z^n$ 表示在 $t\in[0,T]$ 时刻每个车站的负载状况
• 输入：由加权图G=(V,E,c,w)诱导的度量空间M=(V,d)和G中的一个计算旅行时间的最短路径度量d。初始状态每个车站 $v\in V$ 的汽车和司机个数 $x_v^0$ 。司机总数k，车队最多汽车数C(可拖车)。顾客预订的请求序列 $\sigma=(r_1,\cdots,r_h)$ ，接收请求 $r_i$ 的利润 $p_i$ 。
• 输出：是否拒绝 $\sigma$ 中的请求，一个重分配汽车的计划
• 目标：最大化利润，最小化重分配汽车的消耗

离线带重分配的最大接收问题对应一个时间展开重分配网络(time-expanded relocation network) $N_{rel}(\sigma)=(V,A)$ ，$V=s^+\cup\{(v,t):v\in V,t\in [0,T]\}\cup s^-$ ， $A=A_+\cup A_P \cup A_\sigma \cup A_L \cup A_-$ ，其中源边(source arc) $(s^+\to (v,0))\in A_+,\forall v\in V$ ，停车边(park arc) $((v,t)\to (v,t+1))\in A_P, \forall v\in V,t\in [0,T)$ ，请求边(request arc) $((v^{pick}_i,t^{pick}_t)\to(v^{drop}_i,t^{drop}_i))\in A_\sigma,\forall r_i\in\sigma$ ， 重分配边(relocation arc)$若 d(v,v')=t'-t, ((v,t)\to(v',t'))\in A_L$ 表示所有重分配车队的移动，漏边(sink arc) $((v,T)\to s^-)\in A_-,\forall v\in V$

因此离线带重分配的最大接收问题被转化为了此网络上汽车流f和司机流F的耦合最大流(coupled flows)问题，得到ILP：

$\max \sum_{a\in A_\sigma} p_a f_a - \sum_{a\in A}w_a F_a\\ s.t.\ \sum_{a\in \delta^+(s^+)} f_a=x^0_v, \sum_{a\in \delta^+(s^+)} F_a=x^0_v\\ \sum_{a\in \delta^-(v,t)} f_a=\sum_{a\in \delta^+(v,t)} f_a,\sum_{a\in \delta^-(v,t)} F_a=\sum_{a\in \delta^+(v,t)} F_a,\forall(v,t)\\ f_a\leq c_v,\forall a\in A_P\\ f_a\leq 1, F_a\leq 0, \forall a\in A_\sigma\\ f_a\leq CF_a,\forall a\in A_L\\ f_a\in \mathbb Z_+,F_a\in\mathbb Z_+,\forall a\in A$

推论：无重分配(relocation)的离线最大接收问题(Max-Accept Problem)可在多项式时间内解决

推论：有重分配的离线最大接收问题是NP-hard问题

定理(KARP1972)：判断一个给定的图G是否有一个使用k个颜色的涂色是NPC问题

定理(Chudnovsky2004)：一个图是完美(perfect)的当且仅当它不包含奇数洞(odd holes) $C_{2k+1}$ 或奇数逆洞(odd antiholes)$\bar C_{2k+1}$， $k\geq 2$ 作为诱导(induced)子图。

引理：对任意图G，有 $\chi(G)\leq\Delta(G)+1$ ，其中 $\Delta(G)$ 是G的最大度数

定理(Brooks1941)：如果G不是一个团(clique)或无弦的奇环路(chordless odd cycle)，则 $\chi(G)\leq \Delta(G)$

区间颜色数(Interval chromatic number)：给定节点加权的图G=(V,E,w)，和一个区间染色 $\mathcal I$，此区间染色的长度(span)定义为 $s(\mathcal I)=\max\{ r(v): v\in V\}-\min\{ l(v): v\in V\}$ 。所有区间染色的最小长度是它的颜色数，记为$\chi_\mathcal I (G,w)$

区间染色问题(Interval coloring problem)：给定节点加权的图G=(V,E,w)，找到一个区间染色(interval coloring) $\mathcal I$ 使长度为 $\chi_\mathcal I (G,w)$

定理(Kubale)：判断一个图是否有一个长度为k的区间染色是NPC问题

加权团数(weighted clique number)：考虑一个加权的图G=(V,E,w)，则加权团数是 $\omega(G,w)=\max\{w(Q):Q\subseteq G\ clique\}\leq\chi_{\mathcal I}(G,w)$ ，它是图G的区间颜色数(chromatic number)的下界

超完美图(super-perfect graph)：若图G=(V,E,w)的任意诱导子图 $G'\subseteq G$ 和任意整数权重w，都有 $\omega(G',w)=\chi_{\mathcal I}(G',w)$

结论：频率分配问题(Frequency allocation problem)是一个特殊的区间染色问题

引理(Marenco, Wagler2007)：频率分配问题存在DegreeGreedy，DemandGreedy，CombinGreedy，RandomGreedy等启发规则和ENUMERATOR的精确解

• Integration by parts(Green's first identity): $$\int_\Omega (v\nabla\cdot U + U \cdot \nabla v) dx=\int_{\partial \Omega}v(U\cdot \nu)dA$$

M-x xterm-mouse-mode 在命令行中使用鼠标

C-x o 切换至其他窗口

C-x C-b list all buffers
然后
1 C-x o进入清单。2 可以上下移动。
3 在某清单的行上按k或d，清单前面显示D代表该行被标记删除，按u去掉该标记，也可以按s进行存盘标记，按下%立马变为只读标记.
4 按x执行。

C-x r k 剪切一个矩形

C-x r t 插入矩形相同内容

C-q C-j为换行符可替换

C-x C-f "find"文件, 即在缓冲区打开/新建一个文件
C-x C-s 保存文件
C-x C-w 使用其他文件名另存为文件
C-x C-v 关闭当前缓冲区文件并打开新文件
C-x i 在当前光标处插入文件
C-x b 新建/切换缓冲区
C-x C-b 显示缓冲区列表
C-x k 关闭当前缓冲区
C-z 挂起emacs
C-x C-c 关闭emacs
 
光标移动基本快捷键(Basic Movement)
C-f 后一个字符
C-b 前一个字符
C-p 上一行
C-n 下一行
M-f 后一个单词
M-b 前一个单词
C-a 行首
C-e 行尾
C-v 向下翻一页
M-v 向上翻一页
M-< 到文件开头
M-> 到文件末尾
 
编辑(Editint)
M-n 重复执行后一个命令n次
C-u 重复执行后一个命令4次
C-u n 重复执行后一个命令n次
C-d 删除(delete)后一个字符
M-d 删除后一个单词
Del 删除前一个字符
M-Del 删除前一个单词
C-k 移除(kill)一行
 
C-Space 设置开始标记 (例如标记区域)
C-@ 功能同上, 用于C-Space被操作系统拦截的情况
C-w 移除(kill)标记区域的内容
M-w 复制标记区域的内容
C-y 召回(yank)复制/移除的区域/行
M-y 召回更早的内容 (在kill缓冲区内循环)
C-x C-x 交换光标和标记
 
C-t 交换两个字符的位置
M-t 交换两个单词的位置
C-x C-t 交换两行的位置
M-u 使从光标位置到单词结尾处的字母变成大写
M-l 与M-u相反
M-c 使从光标位置开始的单词的首字母变为大写
 
重要快捷键(Important)
C-g 停止当前运行/输入的命令
C-x u 撤销前一个命令
M-x revert-buffer RETURN (照着这个输入)撤销上次存盘后所有改动
M-x recover-file RETURN 从自动存盘文件恢复
M-x recover-session RETURN 如果你编辑了几个文件, 用这个恢复
 
在线帮助(Online-Help)
C-h c 显示快捷键绑定的命令
C-h k 显示快捷键绑定的命令和它的作用
C-h l 显示最后100个键入的内容
C-h w 显示命令被绑定到哪些快捷键上
C-h f 显示函数的功能
C-h v 显示变量的含义和值
C-h b 显示当前缓冲区所有可用的快捷键
C-h t 打开emacs教程
C-h i 打开info阅读器
C-h C-f 显示emacs FAQ
C-h p 显示本机Elisp包的信息
 
搜索/替换(Seach/Replace)
C-s 向后搜索
C-r 向前搜索
C-g 回到搜索开始前的位置(如果你仍然在搜索模式中)
M-% 询问并替换(query replace)
 
Space或y 替换当前匹配
Del或n 不要替换当前匹配
. 仅仅替换当前匹配并退出(替换)
, 替换并暂停(按Space或y继续)
! 替换以下所有匹配
^ 回到上一个匹配位置
RETURN或q 退出替换
 
使用正则表达式(Regular expression)搜索/替换
可在正则表达式中使用的符号:
^ 行首
$ 行尾
. 单个字符
.* 任意多个(包括没有)字符
< 单词开头
> 单词结尾
[] 括号中的任意一个字符(例如[a-z]表示所有的小写字母)
 
M C-s RETURN 使用正则表达式向后搜索
M C-r RETURN 使用正则表达式向前搜索
C-s 增量搜索
C-s 重复增量搜索
C-r 向前增量搜索
C-r 重复向前增量搜索
M-x query-replace-regexp 使用正则表达式搜索并替换
 
窗口命令(Window Commands)
C-x 2 水平分割窗格
C-x 3 垂直分割窗格
C-x o 切换至其他窗格
C-x 0 关闭窗格
C-x 1 关闭除了光标所在窗格外所有窗格
C-x ^ 扩大窗格
M-x shrink-window 缩小窗格
M C-v 滚动其他窗格内容
C-x 4 f 在其他窗格中打开文件
C-x 4 0 关闭当前缓冲区和窗格
C-x 5 2 新建窗口(frame)
C-x 5 f 在新窗口中打开文件
C-x 5 o 切换至其他窗口
C-x 5 0 关闭当前窗口
 
书签命令(Bookmark commands)
C-x r m 在光标当前位置创建书签
C-x r b 转到书签
M-x bookmark-rename 重命名书签
M-x bookmark-delete 删除书签
M-x bookmark-save 保存书签
C-x r l 列出书签清单
 
d 标记等待删除
Del 取消删除标记
x 删除被标记的书签
r 重命名
s 保存列表内所有书签
f 转到当前书签指向的位置
m 标记在多窗口中打开
v 显示被标记的书签(或者光标当前位置的书签)
t 切换是否显示路径列表
w 显示当前文件路径
q 退出书签列表
 
M-x bookmark-write 将所有书签导出至指定文件
M-x bookmark-load 从指定文件导入书签
 
Shell
M-x shell 打开shell模式
C-c C-c 类似unix里的C-c(停止正在运行的程序)
C-d 删除光标后一个字符
C-c C-d 发送EOF
C-c C-z 挂起程序(unix下的C-z)
M-p 显示前一条命令
M-n 显示后一条命令
 
DIRectory EDitor (dired)
C-x d 打开dired
C(大写C) 复制
d 标记等待删除
D 立即删除
e或f 打开文件或目录
g 刷新当前目录
G 改变文件所属组(chgrp)
k 从屏幕上的列表里删除一行(不是真的删除)
m 用*标记
n 光标移动到下一行
o 在另一个窗格打开文件并移动光标
C-o 在另一个窗格打开文件但不移动光标
P 打印文件
q 退出dired
Q 在标记的文件中替换
R 重命名文件
u 移除标记
v 显示文件内容
x 删除有D标记的文件
Z 压缩/解压缩文件
M-Del 移除标记(默认为所有类型的标记)
~ 标记备份文件(文件名有~的文件)等待删除
# 标记自动保存文件(文件名形如# name# )等待删除
* / 用* 标记所有文件夹(用C-u * /n移除标记)
= 将当前文件和标记文件(使用C-@标记而不是dired的m标记)比较
M-= 将当前文件和它的备份比较
! 对当前文件应用shell命令
M-} 移动光标至下一个用*或D标记的文件
M-{ 移动光标至上一个用*或D标记的文件
% d 使用正则表达式标记文件等待删除
% m 使用正则表达式标记文件为*
+ 新建文件夹
> 移动光标至后一个文件夹
< 移动光标至前一个文件夹
s 切换排序模式(按文件名/日期)
 
或许把这个命令归入这一类也很合适:
M-x speedbar 打开一个独立的目录显示窗口
 
Telnet
M-x telnet 打开telnet模式
C-d 删除后一个字符或发送EOF
C-c C-c 停止正在运行的程序(和unix下的C-c类似)
C-c C-d 发送EOF
C-c C-o 清除最后一个命令的输出
C-c C-z 挂起正在运行的命令
C-c C-u 移除前一行
M-p 显示前一条命令
 
Text
只能在text模式里使用
M-s 使当前行居中
M-S 使当前段落居中
M-x center-region 使被选中的区域居中
 
宏命令(Macro-commands)
C-x ( 开始定义宏
C-x ) 结束定义宏
C-x e 运行最近定义的宏
M-n C-x e 运行最近定义的宏n次
M-x name-last-kbd-macro 给最近定义的宏命名(用来保存)
M-x insert-kbd-macro 将已命名的宏保存到文件
M-x load-file 载入宏
 
编程(Programming)
M C- 自动缩进光标和标记间的区域
M-m 移动光标到行首第一个(非空格)字符
M-^ 将当前行接到上一行末尾处
M-; 添加缩进并格式化的注释
C, C++和Java模式
M-a 移动光标到声明的开始处
M-e 移动光标到声明的结尾处
M C-a 移动光标到函数的开始处
M C-e 移动光标到函数的结尾处
C-c RETURN 将光标移动到函数的开始处并标记到结尾处
C-c C-q 根据缩进风格缩进整个函数
C-c C-a 切换自动换行功能
C-c C-d 一次性删除光标后的一串空格(greedy delete)
 
为了实现下面的一些技术, 你需要在保存源代码的目录里运行"etags
.c .h *.cpp"(或者源代码的其他的扩展名)
M-.(点) 搜索标签
M-x tags-search ENTER 在所有标签里搜索(使用正则表达式)
M-,(逗号) 在tags-search里跳至下一个匹配处
M-x tags-query-replace 在设置过标签的所有文件里替换文本
 
GDB(调试器)
M-x gdb 在另一个的窗格中打开gdb
 
版本控制(Version Control)
C-x v d 显示当前目录下所有注册过的文件(show all registered files in this dir)
C-x v = 比较不同版本间的差异(show diff between versions)
C-x v u 移除上次提交之后的更改(remove all changes since last checkin)
C-x v ~ 在不同窗格中显示某个版本(show certain version in different window)
C-x v l 打印日志(print log)
C-x v i 标记文件等待添加版本控制(mark file for version control add)
C-x v h 给文件添加版本控制文件头(insert version control header into file)
C-x v r 获取命名过的快照(check out named snapshot)
C-x v s 创建命名的快照(create named snapshot)
C-x v a 创建gnu风格的更改日志(create changelog file in gnu-style)

安装

git clone https://github.com/igraph/igraph
cd igraph
./bootstrap.sh
./configure --prefix=$MY_LOCAL
make
make install
export CPATH="$MY_LOCAL/include:$CPATH"
export LD_LIBRARY_PATH="$MY_LOCAL/lib:$LD_LIBRARY_PATH"

示例代码

以下代码创建了一个6个节点的空图，添加了8条边，又添加了2个节点和4条边

%:include <igraph/igraph.h>
int main(void)
{
    igraph_t graph;
    igraph_vector_t edges;
    igraph_real_t data[] = {0,1,0,2,0,5,1,2,1,4,2,4,1,3,3,5};
    igraph_vector_view(&edges, data, sizeof(data)/sizeof(double));

    igraph_empty(&graph, 6, IGRAPH_UNDIRECTED);
    igraph_add_edges(&graph, &edges, 0);

    igraph_add_vertices(&graph, 2, 0);
    igraph_add_edge(&graph, 6,4);
    igraph_add_edge(&graph, 6,5);
    igraph_add_edge(&graph, 7,5);
    igraph_add_edge(&graph, 7,3);

    printf("vertices: %d, edges: %d\n", (int)igraph_vcount(&graph), (int)igraph_ecount(&graph));

    igraph_destroy(&graph);
    return 0;
}

使用如下命令编译

gcc test.c -ligraph