• Integration by parts(Green's first identity): $$\int_\Omega (v\nabla\cdot U + U \cdot \nabla v) dx=\int_{\partial \Omega}v(U\cdot \nu)dA$$

如何将标准主问题转化为对偶问题？

定理：主问题(P)

$$ \begin{align*} &\max && c^\top x \\ &s.t. && Ax=b \\ & && x\geq0 \end{align*} $$

的对偶问题(D)为

$$ \begin{align*} &\min && b^\top y \\ &s.t. && A^\top y\geq c \end{align*} $$

任何线性规划问题都可以写成标准形式，如下例：
非标准形式(P1)

$$ \begin{align*} &\max && d^\top x \\ &s.t. && Fx=0 \\ & && Ix\leq c \\ & && x\geq0 \end{align*} $$

引入松弛变量$x^\prime$，则有标准形式(P)

$$ \begin{align*} &\max && \begin{bmatrix}d\\0\end{bmatrix} ^\top \begin{bmatrix}x\\x^\prime\end{bmatrix} \\ &s.t. && \begin{bmatrix}I & 1\\F & 0\end{bmatrix}\begin{bmatrix}x\\x^\prime\end{bmatrix}= \begin{bmatrix}c\\0\end{bmatrix} \\ & && \begin{bmatrix}x\\x^\prime\end{bmatrix}\geq0 \end{align*} $$

使用以上定理可以很容易得到对偶问题

对于最小化问题，可以先转为最大化问题再使用以上定理，也可以直接使用以下定理
定理：主问题(P)

$$ \begin{align*} &\min && c^\top x \\ &s.t. && Ax=b \\ & && x\geq0 \end{align*} $$

则有对偶问题(D)

$$ \begin{align*} &\max && b^\top y \\ &s.t. && A^\top y\leq c \end{align*} $$

数学分析

1. 当题目中有关于积分的不等式时，可以考虑构造一个原函数$F(x)$使$F^{\prime}(x)$有不等式的形式，如$F(x)=x\int_{x}^{1}f(y)dy$或直接求它的导函数$f^{\prime}(x)$；使用积分中值定理（与积分面积相等的矩形必与曲线相交于一点$(\xi,f(\xi))$）
2. 当题目中有等式或函数某点值时，可考虑拉格朗日中值定理和罗尔定理.（拉格朗日中值定理与一阶泰勒公式等价.）
3. 题目中有定积分时可考虑将常数项凑成定积分.
   
4. 注意定义域.
5. $$(\ln(x+\sqrt{x^{2}\pm1}))^{\prime}\\=\frac{1}{\sqrt{x^{2}\pm1}}$$ $$(\arcsin x)^{\prime}\\=\frac{1}{\sqrt{1-x^{2}}}$$ $$(\frac{1}{2}x\sqrt{x^{2}\pm1}\pm\frac{1}{2}\ln|x+\sqrt{x^{2}\pm1}|)^{\prime}\\=\sqrt{x^{2}\pm1}$$ $$(\frac{1}{2}x\sqrt{1-x^{2}}+\frac{1}{2}\arcsin x)^{\prime}\\=\sqrt{1-x^{2}}$$(可用dx中的x分部积分得出)
6. 分部积分时设积分结果为$I$，要尽量凑出$I$以构成关于$I$的方程，如$I=\int_{0}^{\frac{m\pi}{2}}\sin^{n}xdx$要尽量使右侧出现$\sin x$.
7. 能用三角解决的不要用无理式，有$\sin^{2}x$，$\cos^{2}x$可凑$\tan^{2}x$，有$\frac{1}{\cos^{2}x}dx$可凑$d(\tan x)$，有$\sqrt{1-x^{2}}$可换$\sin t$，想办法凑$\tan t$.
8. $\int\frac{du}{(\frac{u}{2})^{2}+1}\neq\arctan\frac{u}{2}$不要忘记积分变量与变量一致性.
9. 积分结果一定要求导验证.
10. 能拆出常数项或多项式项的要先拆后积分，如$$\int\frac{du}{(2u-1)(u^{2}+1)}=\int\frac{u^{2}+1-u^{2}}{(2u-1)(u^{2}+1)}du$$ 从高阶开始配凑，也可使用待定参数，令$$\frac{1}{(2u-1)(u^{2}+1)}=A\frac{1}{2u-1}+B\frac{u}{u^{2}+1}+C\frac{1}{u^{2}+1}$$解得$$A=\frac{4}{5},B=-\frac{2}{5},C=-\frac{1}{5}$$
    归纳：分母要化为$$(A_{1}x+B_{1})^{n}(A_{2}x^{2}+B_{2})(A_{3}x^{2}+B_{3}x+C_{3})$$时，若后两式不能因式分解则最简分量必有$$\frac{1}{(A_{1}x+B_{1})^{n}},\frac{x}{A_{2}x^{2}+B_{2}},$$ $$\frac{1}{A_{2}x^{2}+B_{2}},$$ $$\frac{x}{A_{3}x^{2}+B_{3}x+C_{3}},\frac{1}{A_{3}x^{2}+B_{3}x+C_{3}}$$.
11. 柯西不等式$[\int_{a}^{b}f(x)g(x)dx]^{2}\leq\int_{a}^{b}[f(x)]^{2}dx\cdot\int_{a}^{b}[g(x)]^{2}dx$.
12. 直线$l$ $\frac{x-x_{0}}{a}=\frac{y-y_{0}}{b}=\frac{z-z_{0}}{c}$方向向量为$\vec{l}=(a,b,c)$，经过点$L(x_{0},y_{0},z_{0})$，点 $M$ 到 $l$ 的距离为 $d=\frac{|\vec{l} \times \vec{L}|}{|\vec{l}|}$ .
13. 一条直线与另外两条直线相交，它们的方向向量没有直接关系，也不能联立两直线求交点，认为它在第三条直线上，因为交点可能有两个.
14. 若$f(x,y)$在$(x,y)$点可微，则$f(x+\Delta x,y+\Delta y)-f(x,y)=f'_{x}(x,y)\Delta x+f'_{y}(x,y)\Delta y=O(\sqrt{(\Delta x)^{2}+(\Delta y)^{2}})$.
15. $\frac{d}{dy}f(0,y)|_{y=0}=\lim\limits_{\Delta y\to0}\frac{f(0,\Delta y)-f(0,0)}{\Delta y}=\lim\limits_{\Delta y\to0}[\frac{f(x,\Delta y)-f(x,0)}{\Delta y}]_{x=0}=\frac{\partial}{\partial y}f(x,y)|_{(0,0)}$，因此可在求偏导前对无关变量赋值.
16. 设$\vec{l}$与$x,y,z$轴夹角分别为$\alpha,\beta,\gamma$，则函数$u(x,y,z)$沿$\vec{l}$方向的方向导数为
    $$ \frac{\partial u}{\partial\vec{l}}=\frac{\partial u}{\partial x}\cos\alpha+\frac{\partial u}{\partial y}\cos\beta+\frac{\partial u}{\partial z}\cos\gamma $$.
17. $[f(u(x,y),v(x,y))]_{x}^{\prime}=f_{1}^{\prime}u_{x}^{\prime}+f_{2}^{\prime}v_{x}^{\prime}.$
18. $u(x,y,z)$在$\nabla u$方向上的方向导数最大，值为$|\nabla u|$.
19. $f_{x}^{\prime}(x,y,z)$ $(z=z(x,y))$ $\neq$ $\frac{\partial}{\partial x}[f(x,y,z(x,y))]$.
20. $\varphi_{x}^{\prime}(2x^{2})=\varphi^{\prime}(2x^{2})\cdot4x$.
21. 当$f_{12}^{\prime\prime}=f_{21}^{\prime\prime}$时,最后结果应合并.
22. 隐函数求导之前应将所有$z=z(x,y)$标记出来以免遗忘.
23. 多项式要统一格式，如$x-y,y-x$应统一为$x-y,-(x-y)$.
24. 求导要一步一步地求，不要跳步.
25. 对$f(x,y)=0$可用全微分为0得到$\frac{dy}{dx}=-\frac{f_{x}^{\prime}}{f_{y}^{\prime}}$.
26. $\frac{\partial(x,y)}{\partial(u,v)}$
    $=\begin{pmatrix}\frac{\partial x}{\partial u} & \frac{\partial x}{\partial v}\\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v}\end{pmatrix}$
    $=\begin{pmatrix}\frac{\partial x}{}\\ \frac{\partial y}{}\end{pmatrix}\begin{pmatrix}\frac{}{\partial u} & \frac{}{\partial v}\end{pmatrix}$.
27. 曲线$(x(t),y(t),z(t))$在$(x,y,z)$点切线方向向量为$(x^{\prime},y^{\prime},z^{\prime})$.
28. 曲面$f(x,y,z)=0$在$(x,y,z)$点法线方向向量为$(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z})$.
29. $\vec{a}=(x_{1},y_{1},z_{1})$，$\vec{b}=(x_{2},y_{2},z_{2})$方向相同$\Rightarrow$ $\frac{x_{1}}{x_{2}}=\frac{y_{1}}{y_{2}}=\frac{z_{1}}{z_{2}}$ $\nRightarrow$ $\begin{cases}x_{1}=x_{2}\\y_{1}=y_{2}\\z_{1}=z_{2}\end{cases}$
30. 求函数在曲面上的最值(条件最值)，因最值点一定在曲面上，可将曲面作为乘子引入，令$F=(\ln)f(x,y,z)+\lambda\cdot g(x,y,z)$(拉格朗日乘子法).
31. 海伦公式：$S=\sqrt{\frac{L}{2}(\frac{L}{2}-a)(\frac{L}{2}-b)(\frac{L}{2}-c)}$.
32. $z(x,y)$在$(x_{0},y_{0})$处满足$\frac{\partial z}{\partial x}=\frac{\partial z}{\partial y}=0$，$A=\frac{\partial^{2}z}{\partial x^{2}},B=\frac{\partial^{2}z}{\partial x\partial y},C=\frac{\partial^{2}z}{\partial y^{2}}$，若：1.$B^{2}-AC<0$, $1^{\circ}$.$A>0$，取极小值，$2^{\circ}$.$A<0$，取极大值；2.$B^{2}-AC>0$，非极值点.
33. 对$f(x,y)$若$\frac{\partial^{2}f}{\partial x\partial y}=0$，则$\frac{\partial f}{\partial y}=\int0dx=\varphi(y)$，$f=\int\varphi(y)dy=\psi(y)+C(x)$，对变量$x$积分会出现$\varphi(y)$.
34. 不要把法向量与$(\frac{\partial F}{\partial x},\frac{\partial F}{\partial y},\frac{\partial F}{\partial z})$划等号，它们是共线关系.
35. 多重积分时，$x$的上下限为区域画横线，$y$的上下限为区域画竖线.
36. 曲面面积$S=\iint\sqrt{1+(z_x^{\prime})^2+(z_y^{\prime})^2}\mathrm{d}x\mathrm{d}y$
37. $(x^2)^{\frac{3}{2}}\neq x^3$
38. 函数奇偶性，周期性结合积分上下限可极大简化运算
39. 多重积分$ \int \mathrm{d}x \int \mathrm{d}y \int f \mathrm{d}z$中y的上下限由对z积分后降维图形区域范围确定
40. 转动惯量$ I=\iiint r^2\rho\mathrm{d}V$
41. 开根号一定要加绝对值
42. 不要轻易破坏对称性用于化简，如$ \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\sin\theta\cos^3\theta\mathrm{d}\theta$因$\sin\theta\cos^3\theta$为奇，得积分为0
43. $\int_C P\mathrm{d}x+Q\mathrm{d}y$与路径无关$\Leftrightarrow\oint_CP\mathrm{d}x+Q\mathrm{d}y =0\Leftrightarrow P\mathrm{d}x+Q\mathrm{d}y=\mathrm{d}u\Leftrightarrow\frac{\partial Q}{\partial x}=\frac{\partial P}{\partial y}$，设$\vec{F}=(P(x,y,z),Q(x,y,z),R(x,y,z)),\\ \mathrm{d}\vec{l}=(\mathrm{d}x,\mathrm{d}y,\mathrm{d}z),\\ \oint_L\vec{F}\mathrm{d}\vec{l}=\oint_LP\mathrm{d}x+Q\mathrm{d}y +R\mathrm{d}z =\iint_\Sigma\nabla \times\vec{F}\cdot\mathrm{d}\vec{\sigma}$
    对于可分离出保守场的积分要进行分离以简化运算
44. 设平面$\Sigma(x,y,z)$法向量为$\vec{p}=(A,B,C)$面积为S，则它在$\vec{n}=(\alpha,\beta,\gamma)$方向降维后面积为$S^{\prime}=S\frac{\vec{n}\cdot\vec{p}}{|\vec{n}|\cdot|\vec{p}|}$，其中$\vec{p}$的方向与围成$\Sigma$的封闭曲线有关，从z轴正向看即从z的正无穷处向下看，逆时针则$\vec{p}$向上
45. 求体积分和平面积分时，不要用边界条件化简被积函数
46. 无穷级数若可展开为$\frac{1}{n}+\frac{1}{n^2}+\cdots$则应展开后根据最低阶判断收敛性（比较判别法的极限形式）没有$\frac{1}{n}$可先凑出$\frac{1}{n}$；可积分时使用积分判别法；带有$p^n$时考虑$\lim\limits_{n\to\infty}\sqrt[n]{a_n}$判别（根值判别法）
47. 使用洛必达后再用级数展开会引起系数错误，如$1-\frac{\sin x}{x}$

48. 交错级数：

    1. 求$\lim\limits_{n\to\infty}|a_n|$，不为0则不收敛，再看是否绝对收敛
    2. 求$a_n$与$a_{n+1}$大小关系，若$a_n>a_{n+1}$，条件收敛
49. $\sum\limits_{n=1}^{+\infty}\frac{1}{n}=\ln n+c+r_n$，c为欧拉常数，$r_n\to0,\sum\limits_{n=1}^{\infty}\frac{1}{n^2}=\frac{\pi^2}{6}$
50. $\because \frac{\ln n}{n}>\frac{1}{n}, (n\geq3), \therefore\sum\limits_{n=1}^{+\infty}\frac{\ln n}{n}$发散
51. 一阶线性微分方程$\frac{\mathrm{d}y}{\mathrm{d}x}+P(x)y=Q(x)$先解齐次方程通解$y=C_1e^{-\int P(x)\mathrm{d}x}$令$C_1=C_1(x)$将通解代入非齐次方程得$y=e^{-\int P\mathrm{d}x}[c+\int Q\mathrm{e}^{\int P\mathrm{d}x}\mathrm{d}x]$
52. 复杂级数先求导或积分再求幂级数
53. $b_n=\frac{2}{T}\int_0^Tf(x)\sin\frac{n\pi x}{T}\mathrm{d}x$ （延拓）， $b_n=\frac{2}{2T}\int_{-T}^Tf(x)\sin\frac{n\pi x}{T}\mathrm{d}x$
54. 和差化积$$\sin\alpha+\sin\beta=2\sin\frac{\alpha+\beta}{2}\cos\frac{\alpha-\beta}{2}\\ \cos\alpha+\cos\beta=2\cos\frac{\alpha+\beta}{2}\cos\frac{\alpha-\beta}{2}$$
55. 解一阶非线性方程时，将x和y凑到一起再进行换元，如$(x+y)y^{\prime}+(x-y)=0$ ，令$u=\frac{y}{x},y^\prime=\frac{u-1}{u+1}$
56. 定积分不要忘记减下限
57. $P(y,x)\mathrm{d}x+Q(y,x)\mathrm{d}y=0$形式的方程：先看$\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}$是否成立，成立则用线积分，或考虑积分因子；再看是否可化为$y^\prime+Py=Q$形式，可以就用公式；最后看是否可分离变量，换元
58. 曲率$\kappa={|\frac{\mathrm{d}\alpha}{\mathrm{d}s}|}=\frac{\mathrm{d}(\arctan y^\prime)}{\sqrt{1+y^{\prime2}}\mathrm{d}x}=\frac{|y^{\prime \prime}|}{(1+y^{\prime2})^{\frac{3}{2}}}$
59. 方程$y^{\prime \prime}+Py^\prime+qy=P_m(x)\mathrm{e}^{ax}$，特解为$y^*=x^kQ_m(x)\mathrm{e}^{ax}$,k为$\mathrm{e}^{ax}$根重数，m为阶数
60. 方程$y^{\prime \prime}+Py^\prime+qy=P_m(x)\mathrm{e}^{ax}\sin bx$，特解为$y^*=x^k(R_m(x)\cos bx + S_m(x)\sin bx)\mathrm{e}^{ax}$，k与a无关，k为$a+ib$的根重数
61. 解伯努利方程$y^\prime+P(x)y=q(x)y^n$应令$z=y^{1-n}$ ；解欧拉方程$x^2\frac{\mathrm{d}^2y}{\mathrm{d}x^2}+a_1x\frac{\mathrm{d}y}{\mathrm{d}x}+a_2y=f(x)$ ，令$x=\mathrm{e}^t$
62. 逆序数：从左到右每个数右边小于它的个数之和
63. $\int_0^{+\infty}\frac{f(x)}{x^p}\mathrm{d}x=\lim\limits_{\epsilon\to0}\int_\epsilon^{1}\frac{f(x)}{x^p}\mathrm{d}x+\lim\limits_{N\to+\infty}\int_1^{N}\frac{f(x)}{x^p}\mathrm{d}x$可判断敛散性，利用极限由洛必达法则还可求出等价积分式；当p<1时，$\int_0^1\frac{1}{x^p}\mathrm{d}x$存在，当p>1时，$\int_1^{+\infty}\frac{1}{x^p}\mathrm{d}x$存在
64. 前n-1阶导数为0，第n阶不为0$\begin{cases}若n为奇，拐点\\若n为偶，极值点\end{cases}$
65. 拐点只能在二阶导数为0或不存在的点取到；极值点只能在驻点或导数不存在的点取到
66. $f(x,y)$在$(x,y)$点最大方向导数为$|\vec{\nabla}f|$（模）
67. 代数运算时应把x写在一起，把y写在一起减少失误
68. 出现$f(x)+f^\prime(x)$时考虑构造$g(x)=f(x)\mathrm{e}^x$
69. 解非齐次线性方程组时不要直接找线性无关解向量，应先转化为齐次线性方程组找到线性无关解再结合特解得到通解
70. $S=\frac{1}{x}\sum\limits_{n=0}^{\infty}\frac{x^{2n+1}}{2n+1}\neq\int\frac{1}{x}\sum\limits_{n=0}^{\infty}x^{2n}\mathrm{d}x$提出的x在求导时会影响结果，应令$S=\frac{1}{x}f(x),f^{\prime}(x)=\sum\limits_{n=0}^{\infty}x^{2n}$
71. $+\infty$和$-\infty$可能对应两条水平渐近线或一条，奇点处常有一条垂直渐近线，有两条水平渐近线就不可能有斜渐近线
72. $f(x,y)$在$(x_0,y_0)$可微$\Leftrightarrow\Delta z=z_x^\prime\Delta x+z_y^\prime \Delta y+O(P)\Leftarrow f^\prime_x, f^\prime_y连续$
73. 读题要仔细，不要把$\mathrm{e}^{x^2}$看成$\mathrm{e}^{-x^2}$
74. 分清收敛区间（开区间）和收敛域
75. 单调有界$\Rightarrow$收敛
76. $\frac{f(x)}{\vec{n}} = \nabla f(x)^T \vec{n}$
77. 鞍点$(x_0,y_0)$：$f(x,y_0)\leq f(x_0,y_0)\leq f(x_0,y)$
78. $\sum_{i}^{}\sum_{j}A_{ij}X_{i}X_{j} = \sum_{i}^{}\sum_{j}X_{i}A_{ij}X_{j} = \sum_iX_i \sum_jA_{ij}X_j = \sum_iX_i[AX]_i = X^T[AX]$
79. 矩阵微积分方法：先正常求导，注意非交换性，再对结果取转置。求导法则：$dy=\mathrm{tr}(\frac{dy}{d\mathbf{X}}d\mathbf{X})$，$d({\mathbf{X}\otimes\mathbf{Y}})=(d\mathbf{X})\otimes\mathbf{Y}+\mathbf{X}\otimes(d\mathbf{Y})$，$d({\mathbf{X}\odot\mathbf{Y}})=(d\mathbf{X})\odot\mathbf{Y}+\mathbf{X}\odot(d\mathbf{Y})$，$d(\mathbf{X}^{-1})=-\mathbf{X}^{-1}(d\mathbf{X})\mathbf{X}^{-1}$，$d(\mathrm{tr}(\mathbf{X}))=\mathrm{tr}(d\mathbf{X}))$ ，$d(|\mathbf{X}|)=\mathrm{tr}(adj(\mathbf{X})d\mathbf{X})=|\mathbf{X}|\mathrm{tr}(\mathbf{X}^{-1}d\mathbf{X})$ ，$df(x,\mathbf{y},\mathbf{Z})=\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial \mathbf{y}}d\mathbf{y}+\mathrm{tr}(\frac{\partial f}{\partial \mathbf{Z}}d\mathbf{Z})$ 例子： $\dfrac{\partial (b^Tx)}{\partial x} = (\dfrac{b^T dx}{dx})^T = b$ , $\dfrac{\partial (x^TAx)}{\partial x} =(\dfrac{d(x^T)Ax+x^TAdx}{dx})^T=(\dfrac{x^TA^Tdx+x^TAdx}{dx})^T= (A+A^T)x$ 其中，$\odot$是Hadamard积，$\otimes$是Kronecker积

线性代数

1. 左/右乘逆矩阵$\Leftrightarrow$增广行/列变换；行/列增广时，逆矩阵的原矩阵的放在左边/上边
2. 行列式为0$\Leftrightarrow$齐次线性方程组有非0解
3. 齐次线性方程组可写成列向量线性组合和行向量点乘形式
4. 实对称阵，不同特征值对应的不同特征向量正交
5. 实对称$\Rightarrow$相似于对角阵；n个不同特征值$\Rightarrow$ 相似对角；n个特征向量线性无关$\Leftrightarrow$ 相似对角
6. $\sum\limits_{i=1}^n\lambda_i=\sum\limits_{i=1}^na_{ii}=tri(A),\prod\limits_{i=1}^n\lambda_i=|A|$ ，相似$\Rightarrow$同秩，同特征值，同行列式
7. 设特征向量$\alpha_1,\alpha_2\cdots\alpha_n$对应特征值$\lambda_1,\lambda_2\cdots\lambda_n$ ，则$[\alpha_1\cdots\alpha_n]^{-1}A[\alpha_1\cdots\alpha_n]=\left[\begin{matrix}\lambda_1&\cdots&0\\0&\cdots&0\\\vdots&&\vdots\\0&\cdots&\lambda_n\end{matrix}\right]=\Lambda$
8. 一个特征值至少有一个特征向量
9. $A=\left[\begin{matrix}a&b\\c&d\end{matrix}\right],A^*=\left[\begin{matrix}d&-b\\-c&a\end{matrix}\right],A^{-1}=\frac{1}{ad-bc}\left[\begin{matrix}d&-b\\-c&a\end{matrix}\right]$
10. 标准型可与相似对角阵无关，但满足惯性定律
11. $AX=B$有解$\Leftrightarrow \mathrm{rank}(A)=\mathrm{rank}(\bar{A})$ 其中$\bar{A}=[A|B]$为增广矩阵
12. 绕y轴旋转的绕点会构成一个以y轴为圆心的圆，即$\sqrt{x^2+z^2}=r$，y坐标不变，因此$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\Rightarrow\frac{x^2+z^2}{a^2}-\frac{y^2}{b^2}=1$
13. 非实对称阵无对应的正交对角化阵，即不存在$P^TP=E$，使$P^{-1}AP=\Lambda$（其中A为任一非对称阵）
14. 若$\alpha$为单位向量，即$\alpha^T\alpha=1$，则$\alpha(\alpha^T\cdot\alpha)=\alpha\cdot1=1\cdot\alpha$，即1为$\alpha\alpha^T$的唯一非零特征值
15. 矩阵与对角阵相似时，对角阵中特征值顺序不影响。矩阵A特征值$\lambda_1\cdots\lambda_n$，则$A\sim\left[\begin{matrix}\lambda_1&\cdots&0\\0&\cdots&0\\\vdots&&\vdots\\0&\cdots&\lambda_n\end{matrix}\right]\Leftrightarrow$有n个线性无关特征向量$\Leftrightarrow\lambda_1=\cdots=\lambda_n(=\lambda)$时，$A-\lambda E$秩为n-r（r重根）
16. 平面图形或线图形绕轴旋转应找到三维坐标与平面某长度关系
17. 看到$a_{ij}$先想到转化成矩阵
18. 环——(+乘法逆元)——>体——(+乘法交换律)——>域。域一定是环，二者的差别在于乘法群：一方面集合差一个元素0，另一方面一个是环的乘半群，一个是交换群
19. ${\displaystyle \delta _{\nu _{1}\dots \nu _{p}}^{\mu _{1}\dots \mu _{p}}={\begin{cases}+1&\quad {\text{if }}\nu _{1}\dots \nu _{p}{\text{ are distinct integers and are an even permutation of }}\mu _{1}\dots \mu _{p}\\-1&\quad {\text{if }}\nu _{1}\dots \nu _{p}{\text{ are distinct integers and are an odd permutation of }}\mu _{1}\dots \mu _{p}\\\;\;0&\quad {\text{in all other cases}}.\end{cases}}}$
20. $\frac{\partial x^TAx}{x}\\=\frac{\partial x_i A_j^i x^j}{\partial x^k}\\=\frac{\partial x_i}{\partial x^k}A_j^i x^j+x_i A_j^i \frac{\partial x^j}{\partial x^k}\\=\delta_i^k A_j^i x^j+ x_i A_j^i \delta^{jk}\\=A_j^k x^j+x_i A_j^i \delta^{jk} \delta_{kk} \delta^{kk}\\=A_j^k x^j+x_i A_j^i \delta^{j}_k \delta^{kk}\\=A_j^k x^j+x_i A_k^i \delta^{kk}\\=A_j^k x^j+\delta_{ii}x^i A_k^i \delta^{kk}\\=Ax+A^Tx$

概率论与数理统计

1. 随机事件常用技巧：加一个有的，$(A+B)+B=C+B$；乘一个有的，$(AB)B=CB$；拆成独立事件
2. $C_0^0$不存在，当$P(B)=0$时，$P(A|B)$不存在
3. 贝叶斯公式：$P(H|X)=\frac{P(X|H)P(H)}{P(X)}$ ，其中$P(H|X)$ 是参数的后验概率（posterior），$P(X|H)$ 是似然函数（likelihood/参数的合理性大小），$P(H)$ 是先验概率（prior），$P(X)$ 是证据因子（evidence），用于归一化
4. 切比雪夫大数定律：$P\left\{偏差比\epsilon大\right\}\leq\frac{方差}{\epsilon^2}$；依概率收敛$n\rightarrow+\infty$时，偏差小于任意小常数；切比雪夫大数定律：$n\rightarrow+\infty$时，总偏差的平均值小于任意小常数；伯努利大数定律：为二项分布时大数定律的特例；辛钦大数定律：二项分布且$E(x_i)=\mu$时大数定律的特例；棣莫弗-拉普拉斯中心极限定律：二项分布当n很大时，$\frac{偏差}{标准差}$服从正态分布；列维-林德伯格中心极限定理：$\sqrt{n}\frac{总偏差的平均值}{标准差}$服从正态分布
5. $D(X-Y)=D(X)+D(Y)-2\mathrm{Cov}(x,y)$
6. $\sigma$和$\sigma^2$ 注意区分，指数分布$P(x)=\lambda\mathrm{e}^{-\lambda x},E(X)=\frac{1}{\lambda},D(X)=\frac{1}{\lambda^2}$泊松分布$P(X=k)=\frac{\lambda^k}{k!}\mathrm{e}^{-\lambda},E(X)=D(X)=\lambda$
7. $X+Y\sim N(2\mu,2\sigma^2),X-Y\sim N(0,2\sigma^2)$，X，Y满足独立，正态分布
8. $\int_0^{+\infty}x^n\mathrm{e}^{-x}\mathrm{d}x=n!,\int_0^{+\infty}\frac{x^n}{n!}\mathrm{e}^{-x}\mathrm{d}x=1$
9. 正态分布运算法则：$D(X_1+X_2+X_3)=3\sigma^2,D(X_1+2X_2)=\sigma^2+4\sigma^2$
10. 正态总体的抽样分布中，$\bar{X}$与$S^2$相互独立（$\mu=0,\sigma=1$）$n\bar{X}^2\sim\chi^2(1),(n-1)S^2\sim\chi^2(n),E(\chi^2(n))=n,D(\chi^2(n))=2n$
11. 若$X\sim\chi^2(n)$，则2X不服从$\chi^2$分布，因此先化系数
12. 计算正态分布概率大小要化成标准正态分布再比较
13. 加和规则：$p(X)=\sum\limits_X p(X,Y)$ 乘积规则：$p(X,Y)=p(Y|X)p(X)$
14. 一维正态分布：$f(x)=\frac{1}{\sqrt{2\pi}\sigma}\mathrm{e}^{-\frac{(x-\mu)^2}{2\sigma^2}}$，n维正态分布：$f_n(\vec{x})=\frac{1}{\sqrt{(2\pi)^n\det(\Sigma)}}\exp (-\frac{1}{2}(\vec{x}-\vec{\mu})^T\Sigma^{-1}(\vec{x}-\vec{\mu}))$ 。对二维正态分布，取$x_1=x_0,-\infty<x_2<+\infty$的 一个平面去截此二维分布曲线，得到的函数曲线设为$g(x_2)$，在全空间积分结果不为1，而是$x_1$的边缘概率分布$f_n(x_1)$在$x_1=x_0$点的值
15. 对于一个有K个结点的图，联合概率为$p(\textbf{x})=\prod\limits_{k=1}^Kp(x_k|pa_k)$ ，其中$pa_k$ 表示$x_k$ 的父结点的集合，$\textbf{x}$ 是所有结点的集合
16. 似然函数$L(\theta|\textbf{x})$ 与概率密度函数$f(\textbf{x}|\theta)$ 的唯一区别是似然函数中$\textbf{x}$ 是已知的给定样本点，$\theta$ 是变量
17. 准确率Precision是分为正例的样本中正确比例:$P=\frac{tp}{tp+fp}$ ，召回率Recall是实际为正例的样本中正确比例:$R=\frac{tp}{tp+fn}$ ，F-measure:$\frac{2PR}{P+R}$ ，精确度Accuracy是正确分类的样本占总体的比例:$A=\frac{tp+tn}{tp+fp+tn+fn}$
18. 衡量聚类结果好坏的指标 纯度Purity:$Purity=\frac1N\sum\limits_{i=1}^k\max_j|c_i\cap t_j|$ ，其中k是聚类个数，$c_i$ 是一个聚类，$t_j$ 是实际类 兰德指数Rand:$Rand=\frac{a+c}{n(n-1)/2}$ ，其中a是两点聚在同一类且正确的点对个数，c是两点聚在不同类且正确的点对个数，n是测试集的大小
19. $\prod\limits_{i\in I}(1+x_i)=\sum\limits_{J\subseteq I}\prod\limits_{j\in J}x_j$
20. 离/偏差：deviation 方差：variance 标准差：standard deviation 平均差：mean deviation
21. 皮尔逊相关系数$\rho_{x,y}$ $= \frac{x和y的协方差}{(x的标准差 * y的标准差)} = \frac{\sum\limits_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum\limits_{i=1}^n(x_i-\bar{x})^2}\sqrt{\sum\limits_{i=1}^n(y_i-\bar{y})^2}}$

最优化方法

1. 当$f(x)$满足$f(x_2)-f(x_1)\geq \nabla f(x_1)(x_2-x_1)$ 时，或$\nabla^2 f(x)$ 是半正定阵/正定（特征值$\geq / >$ 0）时，$f(x)$是凸函数/严格凸函数
2. 如果$\frac{\partial f}{\partial x} (x_0,y_0) = \frac{\partial f}{\partial y} (x_0,y_0)=0, \Delta=\{\frac{\partial^2f}{\partial x^2} \frac{\partial^2f}{\partial y^2} - (\frac{\partial^2f}{\partial x\partial y})^2\}_{(x_0,y_0)}$ ，1.若$\Delta>0$且$\frac{\partial^2 f}{\partial x^2} (x_0,y_0) <0 / \frac{\partial^2 f}{\partial y^2} (x_0,y_0)<0$ ，则$(x_0,y_0)$是局部最大值点 2.若$\Delta>0$且$\frac{\partial^2 f}{\partial x^2} (x_0,y_0) >0 / \frac{\partial^2 f}{\partial y^2} (x_0,y_0)>0$ ，则$(x_0,y_0)$是局部最小值点 3.若$\Delta<0$则$(x_0,y_0)$为鞍点
3. 局部极小点处满足下降方向集与可行方向集的交是空集，下降方向与可行方向不在过原点的任何超平面的同一侧，由Gordan引理可得目标函数$f(x)$梯度与约束函数$c_i(x)$梯度关于非负系数线性相关，等式约束组合系数任意，不等式约束组合系数非负，而当$i\in I^*$时，$c_i(x^*)=0$，$i\in I\backslash I^*$时，$\lambda_i^*=0$，即互补松驰条件$\lambda_i^*c_i(x^*)=0$。若将目标函数梯度的系数取定为1，上述条件即KKT条件。
4. 二阶最优性条件即凹凸要求，即拉格朗日函数的二阶梯度在驻点处约束超曲面的切平面所形成的子空间上正定。

机器学习

1. 验证/开发集用于调整超参数，测试集用于检查模型泛化能力
2. 高偏差/偏置（bias）指过多的泛化，过多的假设；高方差（variance）指过多的拟合，过多的参数（过少的假设）
3. RNN的展开图可以从左下往右上看就是从输入到输出

G是群， $a\in G$ 则 $|a|$ 表示a的阶

$a|b$ 表示a整除b，如2|6

$a\perp b$ 表示a和b互素，如 $3\perp 5$

d是r和s的最小公倍数记作 $d=[r,s]$

群G有子群H，群G的阶是可以被子群H的阶整除的，此时我们称[G:H]为H在G下的指数，指数的多少与陪集个数是相同的

对于环)(R,+,·)，已知(R, +)是阿贝尔群。R的子集I称为R的一个右理想，若I满足：

• (I, +)构成(R, +)的子群。
• ∀i ∈ I，r ∈ R，i·r ∈ I。

如果I既是R的右理想又是R的左理想，那么I是R的理想。

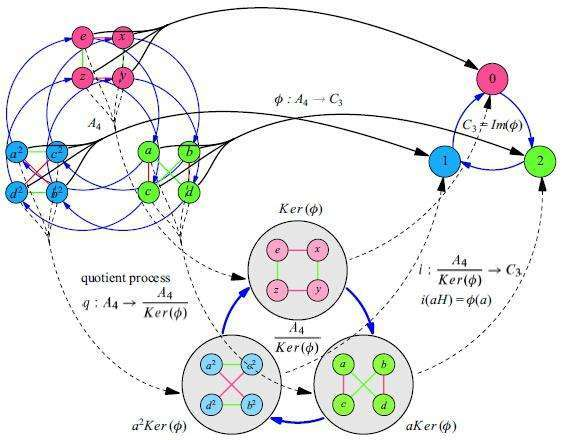
设G是群，H是G的子群，称子群H在群G中的左陪集或右陪集的个数为H在G中的指数，记作 $\left[ {G:H} \right]$ 。拉格朗日定理： $|G| = |H|\left[ {G:H} \right]$

设H是群G的子群，如果对每个 $a\in G$ 都有 $aH=Ha$ 则称H是群G的正规子群，记作 $H \triangleleft G$ ，如果G只有平凡的正规子群，且 $G\neq \{e\}$ 则称G为单群

设G为群，H是G的正规子群，H的所有陪集 $G/H = \{ aH|a \in G\} $ 关于G的子集上的乘法运算构成的群称为G关于H的的商群

环R的理想 P是素理想，当且仅当它是一个真理想（也就是说，P ≠ R），且对于R的任何两个理想A和B，若有AB ⊆ P，则A ⊆ P或B ⊆ P。

任意有单位元的环一定有极大理想，a是R的极大理想当且仅当R/a是单纯环

除环 非零环 整环

在计算反向传播或最优化问题时，经常遇到向量、矩阵、张量对向量、矩阵、张量的求导问题，而类比普通函数求导经常无法处理矩阵转置的问题，因此需要使用一套更简单的符号系统进行运算，即里奇微积分。

爱因斯坦求和约定

相乘时符号相同且共轭的指标，如一个共变自由指标(下标）遇到一个符号相同的反变自由指标（上标），会发生缩并运算成为哑指标，整个表达式自由指标的个数表示最终结果的自由指标个数；当自由指标只有一个 $i$ （如 $x^i,A_i^jx^i=y^j$ ）时，表达式是一个向量（一维张量），有两个 $i,j$ （如 $A_i^j,A^{ij},A_i^jx^j$ ）时，表达式是一个二维张量，以此类推。

符号约定

$R^n$ 表示n维列向量空间， $R^{n*}$ 表示n维行向量空间，$A_{ij}$ 表示双线性映射 $R^n\times R^n\rightarrow R$ ， $A^{ij}$ 表示双线性映射 $R^{n*}\times R^{n*}\rightarrow R$，$x^i$ 表示列向量 $x$， $x_i$ 表示行向量$x^T$（也叫线性泛函或余向量）。

$\delta_i^j$ 是一个单位矩阵， $\delta_{ij}$ 是度量张量（一个双线性映射）， $\delta^{ij}$ 是共轭度量张量，它们有这些性质：$x^j(=x)$ 表示原向量则$\delta_{ij}x^j=x_i(=x^{\top})$ 表示转置向量， $\delta^i_jx^i=\operatorname{diag}(x)$ ， $A_j^i(=A)$ 表示原矩阵则$\delta_{ii}\delta^{jj}A_j^i(=A^\top)$ 表示转置矩阵， $\delta_{ii}\delta^{ii}=1$ ， $\delta_{ij}\delta^{ii}=\delta_j^i$ ，$\frac{dx_i}{dx^j}=\delta_i^j$ ， $\frac{dx^i}{dx^j}=\delta^{ij}$ ， $\frac{dx_i}{dx_j}=\delta_{ij}$ ， $\frac{d X_i^j}{d X_k^l} = \delta^{jl}\delta_{ik}$

矩阵表示与Ricci Calculus表示法的对比

$c = x ^ { \top } y \quad c = x _ { i } y ^ { i }$

$x = A y \quad x ^ { i } = A _ { j } ^ { i } y ^ { j }$

$x ^ { \top } = y ^ { \top } A \quad x _ { j } = y _ { i } A _ { j } ^ { i }$

$C = A \cdot B \quad C _ { k } ^ { i } = A _ { j } ^ { i } B _ { k } ^ { j }$

$A = x y ^ { \top } \quad A _ { j } ^ { i } = x ^ { i } y _ { j }$

$z = x \odot y \quad z ^ { i } = x ^ { i } y ^ { i }$

$A=x\otimes y \quad A^{ij}=x^i y^j$

$C=A\otimes B\quad C^{ij}_{kl}=A_k^i B_l^j$

$B=A\otimes x\quad B_{ij}^k=A_{ij}x^k$

$B = A \operatorname { diag } ( x ) \quad B _ { j } ^ { i } = A _ { j } ^ { i } x _ { j }$

$B = \operatorname { diag } ( x ) A \quad B _ { j } ^ { i } = x ^ { i } A _ { j } ^ { i }$

示例

根据上述原理计算 $x^TAx$ 对 $x$ 的导数：

$\frac{d (x^{\top}Ax)}{dx}$

$=\frac{d (x_i A_j^i x^j)}{d x^k}$

$=\frac{d x_i}{d x^k}A_j^i x^j+x_i A_j^i \frac{d x^j}{d x^k}$

$=\delta_i^k A_j^i x^j+ x_i A_j^i \delta^{jk}$

$=A_j^k x^j+x_i A_j^i \delta^{jk} \delta_{kk} \delta^{kk}$

$=A_j^k x^j+x_i A_j^i \delta^{j}_k \delta^{kk}$

$=A_j^k x^j+x_i A_k^i \delta^{kk}$

$=A_j^k x^j+\delta_{ii}x^i A_k^i \delta^{kk}$

$=Ax+A^{\top}x$

计算 $y\odot (Xw)$ 对 $X$ 的导数：

$\frac{\partial (y\odot (Xw))}{\partial X}$

$=\frac{\partial (y^i X_j^iw^j)}{\partial X_k^l}$

$=y^i\delta^{il}\delta_{jk}w^j$

$=y^i\delta^{il}w_k$

$=\operatorname{diag}(y)\otimes w^\top$

需要注意的是， $\delta_{ii}$ 和 $\delta^{ii}$ 并不像常规的Kronecker符号一样等于n（n是下标对应的维数），而是满足$\delta_{ii}\delta^{ii}=1$ ，它有特殊的用途。在本文中，它主要用于表示矩阵转置。在爱因斯坦约定中，表示矩阵转置是一个容易引起记号混乱的事，如果使用 $A_i^j$ 表示原矩阵（方阵）， $A_j^i$ 表示转置矩阵，那么原本 $A_i^j x^i=y^j$ ，转置后却因为指标无法缩并而无法相乘得到列向量了： $A_j^i ? x^i$ ；此外，不区分上下标的爱因斯坦约定对于这是匪夷所思的。但是根据上面的定义，可以使用 $A_j^i \delta_{ii}\delta^{jj}x^i$ 表示 $A^\top x$ ，而不会产生歧义。事实上，在爱因斯坦约定中，指标只能用于表示张量的各个维，如果张量是对称的，那么不管怎么排列指标，表达式看起来都是一样的，因此本文的参考文献[4]使用了上述 $\delta_{ii}$ 和 $\delta^{ii}$ 符号规避了此问题。

如果你没有看懂本文，没有关系，使用参考文献[4]对应的网站http://matrixcalculus.org/即可在线计算矩阵、张量求导。即使你不懂如何计算爱因斯坦约定，你也可以通过numpy的np.einsum()来帮助你计算爱因斯坦约定，更多有关爱因斯坦约定的内容请参考[10]。

在tensorflow中使用爱因斯坦求和约定可以极大的简化代码，使用以下代码实现矩阵乘法：

$R=A B\quad R_i^k=A_i^j B_j^k$

import tensorflow as tf
R = tf.einsum('ij,jk->ik',A,B)

参考文献

[1] Matrix calculus - Wikipedia

[2] Ricci calculus - Wikipedia

[3] Kronecker delta - Wikipedia

[4] S. Laue, M. Mitterreiter, and J. Giesen. Computing Higher Order Derivatives of Matrix and Tensor Expressions, NIPS 2018.

[5] Einstein notation

[6] Bilinear map - Wikipedia

[7] Linear form - Wikipedia

[8] Covariance and contravariance of vectors

[9] Abstract index notation

[10] Einstein notation and generalized Kronecker symbol

库拉托夫斯基闭包公理可来定义一个集上的拓扑结构，它和以开集作定义拓扑结构的公理等价：

拓扑空间 $(X,\mathrm{cl})$ 是集合X及作用在X的幂集上的闭包算子 $\mathrm{cl}:\mathcal{P}(X)\rightarrow \mathcal{P}(X)$ 且满足以下条件：

• $A\subseteq \mathrm{cl}(A)$
• $ \mathrm{cl}( \mathrm{cl}(A))= \mathrm{cl}(A)$
• $ \mathrm{cl}(A\cup B)= \mathrm{cl}(A)\cup \mathrm{cl}(B)$
• $ \mathrm{cl}(\varnothing)=\varnothing$

A是闭集，如果 $A=\mathrm{cl}(A)$

开集：所有点都是内点，至多可数个开集的并

闭集：开集的余

德语中使用G表示开，F表示闭，δ 表示交，σ表示并

因此Fδ集是闭集的交（有理数集就是一个Fδ集），开集都是Fσ集，闭集都是Gδ集

$\mathcal{B}(X,Y)$ 表示从赋范线性空间X到Y的有界线性算子集。若Y是Banach空间（完备赋范线性空间），则 $\mathcal{B}(X,Y)$ 是Banach空间

$\lim\limits_{n\rightarrow\infty}\frac{1}{n!}\frac{d^n(x^n\ln x)}{dx^n}|_{x=\frac{1}{n}}=\gamma$ 其中 $\gamma$ 是欧拉常数

Do not be seduced by the lotus-eaters into infatuation with untethered abstraction. --The rising sea: foundations of algebraic geometry

范畴论

范畴 $\mathscr{C}$ 由对象 $\mathrm{obj}(\mathscr{C})$ 和态射 $\mathrm{hom}(\mathscr{C})$ 构成。如果一个对象是一个集合，那么态射就是映射，记为 $\mathrm{Sets}$ ； $(S,\geq )$ 也是一个范畴，对象是S中的元素，xy之间存在态射如果存在偏序关系；对于拓扑空间X，$(X,\subset)$ 是一个偏序集，因此也是一个范畴

从A对象到B对象的态射集记为 $\mathrm{Mor}(A,B)$ ，态射复合满足结合律

对每一个对象A都存在恒等态射 $\mathrm{id}_A: A\rightarrow A$

如果态射 $f:A\rightarrow B$ 和 $g:B\rightarrow A$ 复合后得到恒等态射，则f和g是同构

对象A的同构 $f:A\rightarrow A$ 叫做自同构

$\mathscr{A}$ 是 $\mathscr{B}$ 的子范畴，如果 $\mathscr{A}\subset \mathscr{B}$ 且$\mathscr{A}$的态射来自于$\mathscr{B}$，包含所有的恒等态射，且关于复合运算封闭

$F:\mathscr{A}\rightarrow \mathscr{B}$ 是协变函子，如果对于任意$\mathscr{A}$中的态射 $m:A_1\rightarrow A_2$ 和$\mathscr{B}$中的态射 $F(m):F(A_1)\rightarrow F(A_2)$ ，有对任意 $A\in \mathscr{A}$ ， $F(\mathrm{id}_A)=\mathrm{id}_{F(A)}$ ，且保持态射复合运算 $\circ$ ：$F(m_1\circ m_2)=F(m_1)\circ F(m_2)$ 。反变函子会反转复合运算$\circ$：$F(m_1\circ m_2)=F(m_2)\circ F(m_1)$

从向量空间范畴 $\mathrm{Vec}_k$ 到集合范畴 $\mathscr{A}$ 的函子把每个线性变换变成集族$\mathscr{A}$内集合间的映射，额外的向量空间性质丢失，因此这个函子是遗忘函子

基本群是所有从某点出发的环路的同伦（拓扑变形）等价类，乘法由环路的衔接给出（先走一条环路，后走另一条）。X在基点p的基本群记为 $\pi _{1}(X,p)$ 。 圆环 $\mathbb{S}^1$ 的基本群是 $\mathbb{Z}$ ，其元素一一对应于 $e_{m}:t\mapsto e^{2i\pi mt}$ ，其中 $m\in \mathbb {Z}$ 表示环路绕行圆环的次数（计入方向）。

如果一个小范畴（即：对象与全体态射构成一集合）的所有态射皆可逆，则称之为一个广群。所有广群与其间的函子构成一个范畴。群是只有一个对象的广群。

$A\in \mathscr{C}$ ，协变函子 $h^A:\mathscr{C}\rightarrow \mathrm{Sets}$ 把对象 $B\in \mathscr{C}$ 送到 $\mathrm{Mor}(A,B)$ ，把 $f:B_1\rightarrow B_2$ 送到 $\mathrm{Mor}(A,B_1)\rightarrow \mathrm{Mor}(A,B_2)$ ，后者的例子为 $f:B_1\mapsto B_2 \overset {h^A}{\Rightarrow} [g:A\rightarrow B_1]\mapsto [f\circ g:A\rightarrow B_1\rightarrow B_2]$ ；反变函子 $h_A:\mathscr{C}\rightarrow \mathrm{Sets}$ 把对象 $B\in \mathscr{C}$ 送到 $\mathrm{Mor}(B,A)$ ，把 $f:B_1\rightarrow B_2$ 送到 $\mathrm{Mor}(B_2,A)\rightarrow \mathrm{Mor}(B_1,A)$ ，后者的例子为 $f:B_1\mapsto B_2 \overset {h_A}{\Rightarrow} [g:B_2\rightarrow A]\mapsto [g\circ f:B_1\rightarrow B_2\rightarrow A]$，这两种函子称为点函子（functor of points）

如果对所有的 $A,A'\in\mathscr{A}$ ，映射 $\mathrm{Mor}_\mathscr A (A,A')\rightarrow \mathrm{Mor}_\mathscr B (F(A),F(A'))$ 都是一对一的，那么协变函子 $F:\mathscr A \rightarrow \mathscr B$ 是忠实的；如果映射是映上的，那么F是满的，一个既满又忠实的函子是满忠实函子

子范畴 $\mathscr A$的包含函子 $i:\mathscr A\rightarrow \mathscr B$ 是满范畴如果i是满的。包含函子总是忠实的。遗忘函子总是忠实的，但不满；如果A是一个环，那么有限生成A模是范畴 $\mathrm{Mod}_A$ 的满的子范畴

同调函子 $\mathrm H_i(\cdot,\mathbb Z):\mathrm{Top}\rightarrow \mathrm{Ab}$ 是协变函子，余调函子 $\mathrm H^i(\cdot,\mathbb Z):\mathrm{Top}\rightarrow \mathrm{Ab}$ 是反变函子

$\mathscr C$ 的一个对象是始对象如果它有一个到任一对象的映射，是终对象如果它有一个从任一对象来的映射，是零对象如果它既是初始对象又是终止对象

一个积性子集 $S$ 是是环 $A$ 在乘法运算下的闭子集，且包含乘法单位元1；定义环 $S^{-1}A$， 其中的元素 $\frac a s$ 满足 $a\in A,s\in S$ ，且 $\frac{a_1}{s_1}=\frac{a_2}{s_2}\Leftrightarrow \exists s\in S,s(s_2 a_1-s_1 a_2)=0$ ，并定义加法 $\frac{a_1}{s_1}+\frac{a_2}{s_2}=\frac{s_2a_1+s_1a_2}{s_1s_2}$ ，乘法 $\frac{a_1}{s_1}\times \frac{a_2}{s_2}=\frac{a_1a_2}{s_1s_2}$ ，则存在正则环映射 $A\rightarrow S^{-1}A$ 由 $a\mapsto a/1$ 给出； $A\hookrightarrow S^{-1}A \Leftrightarrow$ S不包含零因子（ $\hookrightarrow$ 表示包含映射，即一对一映射）；如果A是一个整环， $S=A-\{0\}$ ，则$S^{-1}A$是A的分式环，记为 $K(A)$

环 $S^{-1}A$是A代数B(环映射 $A\to B$ )作为态射构成的范畴中的始对象，这个范畴中的每个S的元素都被送到B中的可逆元素；换句话说，任何一个把S中每个元素送到可逆元素的映射 $A\to B$ 都可以使用映射 $A\to S^{-1}A$ 进行唯一分解；换句话说，任何一个从 $S^{-1}A$ 出发的映射，和从A出发把S中元素映到可逆元素的映射，是一个东西；此外， $S^{-1}A$ 模和A模是一个东西，同构由 $s\times\cdot:M\to M$ ， $s\in S$ 给出

始态射是逗号范畴中的始对象，其中逗号范畴中的态射为交换块（commutative squares）

泛性质

推出)

拉回

层论

概形论

通用

:= 定义为

$\mathbb{N}:=\{1,2,3,\cdots\}\subseteq\{0,1,2,\cdots\}=:\mathbb{Z}^+$ ， $\mathbb A_K^n:=\langle K^n,K^n,+\rangle$ 是域K上的n维仿射空间，$\mathbb A^n:=\langle \mathbb R^n,\mathbb R^n,+\rangle$ 是n维实仿射空间

$\mathbb{R}^+:=[0,\infty)$ ， $M_{nk}(\mathbb R)$ 表示实n×k维矩阵； $\mathrm M_n(\mathbb C)$ 是n阶复方阵集合

$\mathcal L(E;F)$ 是从向量空间E到F的所有连续线性映射集合，连续线性映射要把单位闭球（ $||u||\leq1$ ）映射到有界集中； $\mathrm{Hom}(E,F)$ 是从向量空间E到F的所有线性映射集合

$\mathrm D f(x)(u)=\mathrm D f_x(u) $

$=df(x)(u)=df_x(u)$

$=f^\prime_x=f^\prime(x)$

$=\left( \frac{\partial f}{\partial x_1}(x) \cdots\frac{\partial f}{\partial x_n}(x) \right)\begin{pmatrix} u_1 \\ \vdots \\ u_n \end{pmatrix}$

观察以上公式可以发现，其实$f:E\to F$ 在 $x\in E$ 处的全微分（Fréchet derivative） $\mathrm D f(x)=\mathrm D f_x=df(x)=df_x$ 是一个线性形式（余向量）， $df_x:\vec E\to \vec F \in \mathrm{Hom}(\vec E,\vec F)$

$f:E\to F$ 在 $x\in E$ 点的 $u\in \vec E$ 方向上的方向导数（Gâteaux derivative） $\mathrm D_u f(x)\in \vec F$

$\mathrm D_u f(a)=\mathrm D f(a)(u)$

集合B的示性函数 $I_B(s):=\left\{ \begin{array}{lcl} 1,\quad &if \quad s\in B\\ 0,\quad &otherwise \end{array} \right. $

$a\wedge b:=\min(a,b)\quad a\vee b:=\max(a,b)$

$\mathfrak{R}z, \mathrm{Re}(z)$ 表示复数z的实部， $\mathfrak{I}z,\mathrm{Im}(z)$ 表示复数z的虚部

概率论

设 $\mathcal{F}$ 是样本空间 $\Omega$ 的集类（由若干子集构成）且满足 $\Omega\in\mathcal F$ 且对有限次集合运算封闭，则 $\mathcal F$ 是样本空间的一个 $\sigma$ 域。若有定义在 $\mathcal F$ 上的集函数 $P:\mathcal F\rightarrow[0,\infty]$ 且满足非负性、完全性、可列可加性，则称 $P$ 是可测空间 $(\Omega,\mathcal F)$ 上的一个概率测度，简称概率，称 $(\Omega,\mathcal F,P)$ 为概率空间，称 $P(A)$ 为事件A的概率，若概率为0的事件的任何子集都属于 $\mathcal F$ ，则称$(\Omega,\mathcal F,P)$为完备的概率空间。随机变量是一个函数 $X:\Omega\rightarrow\mathbb R$ ，随机过程是一个二元单值函数 $X(t,\omega):T\times\Omega\rightarrow\mathbb R$ ，固定样本点 $\omega_0\in\Omega$ ，称 $X(t,\omega_0)$ 为随机过程 $X(t,\omega)$ （ 也可写作$X_t,X_t(\omega),X(t)$ ）的样本函数

CF:特征函数 DF:分布函数 pdf:概率密度函数

$\sigma$ 代数： $\sigma(\mathcal{C})$ ; $\sigma(Y_\gamma:\gamma\in\mathcal{C})$

$E(X;F):=\int_F X \mathrm{d}P$

$E(X/\mathcal{G})$ 条件期望

$x=\uparrow \lim x_n:x_n\uparrow x$ ，即满足 $x_n\leq x_{n+1}(\forall n)且x_n\rightarrow x$

$x=\downarrow \lim x_n:x_n\downarrow x$ ，即满足 $x_n\geq x_{n+1}(\forall n)且x_n\rightarrow x$

$\lim\inf x_n:=\sup\limits_m\{\inf\limits_{n\geq m}x_n\}=\uparrow \lim\limits_m\{\inf\limits_{n\geq m} x_n\}$

$\lim\sup x_n:=\inf\limits_m\{\sup\limits_{n\geq m}x_n\}=\downarrow \lim\limits_m\{\sup\limits_{n\geq m} x_n\}$

$(En,\mathrm{ev}):= \lim\inf E_n:=\mathop\cup_m\mathop\cap_{n\geq m}E_n$

$(E_n,\mathrm{i.o.}):=\lim\sup E_n:=\mathop\cap_m\mathop\cup_{n\geq m}E_n$

$\mathcal L_X,\Lambda_X$ X的分布

$\mathcal L^p, L^p$ 勒贝格空间

$\mathrm{Leb}$ 勒贝格测度

$m\Sigma$ $\Sigma$ -可测函数空间

$M^T$ 在时间T停止的过程

$\langle M \rangle$ 尖括号过程

$\mu(f)$ $f$ 的关于 $\mu$ 的积分

$\mu(f;A):=\int_A f\mathrm{d}\mu$

$\varphi_X$ $X$ 的特征函数

微分几何

设$A=\begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1k} \\ \vdots & \vdots & \vdots & \vdots \\ a_{n1} & \cdots & \cdots & a_{nk}\end{pmatrix} = \begin{pmatrix} A_1 \\ \vdots \\ A_n \end{pmatrix}$ ，$I=(i_1,\cdots,i_k)$ ， $1\leq i_1 < \cdots < i_k \leq n \in \{1,\cdots,n\}$

则定义A的基本k形式表示n维空间中平行六面体投影到k维的体积：$\mathrm{d}x_I(A)=\mathrm{d}x_{i_1} \wedge \cdots \wedge \mathrm{d}x_{i_k}(A)=\mathrm{det}\begin{pmatrix} A_{i_1}\\ \vdots \\ A_{i_k} \end{pmatrix}$

以向量空间 $\mathbb R^n$ 的 $\begin{pmatrix}n \\ k\end{pmatrix}$ 个基本k形式为基底可以构成向量空间 $\wedge^k(\mathbb R^n)$

k形式 $\omega$ 是一个多重线性实值函数 $\omega: M_{nk}(\mathbb R)\rightarrow \mathbb R$ ，它是$\wedge^k(\mathbb R^n)$中的一个向量

$A=(A_1,\cdots,A_{k+l})$ 是一个N×(k+l)矩阵， $\tau$ 是k形式， $\omega$ 是l形式，则：

$\tau \wedge \omega(A)=\sum\limits_{\sigma\in S(k,l)}(-1)^{sign(\sigma)}\tau(A_{\sigma(1)},\cdots,A_{\sigma(k)})\omega(A_{\sigma(k+1)},\cdots,A_{\sigma(k+l)})$

微分k形式 $\omega = \sum\limits_{\text{all possible }I}f_I \mathrm d x_I$ ，微分0形式就是一个可微函数

外微分d是从k形式到k+1形式的映射 $\mathrm d:k\text{-forms}\rightarrow (k+1)\text{-forms}$ ，给定以上定义的微分k形式 $\omega$ ，外微分 $\mathrm d \omega=\sum\limits_{\text{all possible }I}\mathrm d f_I\wedge\mathrm d x_I$ ，其中 $f_I$ 是微分0形式， $\mathrm d f_I=\sum\limits_{i\in I} \frac{\partial f}{\partial x_i}\mathrm d x_i$

给定一个流形M的参数化映射 $\phi:R^k \supseteq B\rightarrow M$ ，它在点p的切空间 $T_p(M)$ 的基底是雅可比矩阵 $D\phi$ 中的列向量，且有 $\int_M \omega=\int_B \omega(D\phi)\mathrm d u_1\cdots\mathrm d u_k$

$\int_M \mathrm d \omega=\int_{\partial M}\omega$

代数

（k,l）shuflle是置换群 $S_n,(n:=k+l)$ 的一个置换 $\sigma$ ，满足 $\sigma(1)<\sigma(2)<\cdots<\sigma(k),\sigma(k+1)<\sigma(k+2)<\cdots<\sigma(k+l)$

$sign(\sigma)=\left\{ \begin{array}{lcl} 0, \quad \text{if }\sigma\text{ is even }\\ 1, \quad \text{if }\sigma\text{ is odd}\end{array} \right.$

$\sim$ 是集合S的一个等价关系，对 $\forall a\in S$ ，S的一个等价类 $[a]=\{x\in S|x\sim a\}$ ，S在等价关系下的商集是S的全体等价类的集合，记作 $S/\sim$

$\mathrm{GL}(n,\mathbb R)$ 是n阶广义线性群， $\mathrm{GL}(n,\mathbb R) \subseteq M_{n}(\mathbb R)$ ； $\mathrm{GL}(V)$ 是从向量空间V到V的线性变换群；如果$\mathrm{GL}(n,\mathbb R)$的元素$A$满足$\mathrm{det}(A)=1$，叫做特殊线性群，记为$\mathrm{SL}(n,\mathbb R)$；满足$QQ^\top=Q^\top Q=I_n$的n阶实矩阵关于矩阵乘法构成的群叫正交群，记为$\mathbf{O}(n, \mathbb R)$；如果$\mathrm{det}(Q)=1$，则称为特殊正交群，记为$\mathbf{SO}(n, \mathbb R) $

参考文献

[1] 应用随机过程 白晓东 ISBN：978-7-302-50734-5 O211.6

[2] 概率和鞅 戴维·威廉姆斯著 郑坚坚译 ISBN：978-7-312-04368-0 O21