对NP-hard问题，有几种处理方法：

• 为问题实例添加限制，相当于利用问题中的特殊结构简化问题
• 寻找精确算法
• 寻找近似算法

实例研究：

最大独立集(稳定集)问题：假设无向图G=(V(G),E(G))是无环的，求最大独立集 $I\subseteq V(G)$

若对于任意线性序列(linear ordering)，贪心算法都能找到最大独立集，则称此图是拟阵的(matroidal)

完美消除序列(Perfect Elimination Ordering)是一个 $V(G)$ 中的一个序列 $x_1,\cdots,x_n$ ，使得 $\forall 1\leq i\leq n$ ， $x_i$ 是 $G[\{x_i,\cdots,x_n\}]$ 中的简单点(simplicial vertex)。其中 $G[X]=(X,E(G)\cap X\times X)$ 是G的导出子图。

推论：任意区间图都有一个完美消除序列

定理：可以在多项式时间内得到区间图的一个区间表示，从这个区间表示可以得到一个完美消除序列

恰当染色(proper coloring)对应一个将顶点分为独立集的划分

色数(chromatic number)是最小的恰当染色的颜色数

定理：给定图G的一个完美消除序列，贪心染色算法使用的颜色数等于最大团的大小

分裂图(split graph)是可以划分成一个团和一个独立集的图

弦图(chordal graph)是没有一个长度大于4的环作为导出子图的图(顶点数大于3的环至少有一个弦)，弦图都是完美图

推论：每个分裂图都有完美消除序列。分裂图既是弦图，又是弦图的补图

定理：G有一个完美消除序列，当且仅当它是一个弦图

$S\subseteq V(G)$ 是一个分离子(separator)如果 $G[V(G)\setminus S]$ 有比G更多的连通分量

S是最小分离子，如果S是分离子且对任意 $x\in S$ ， $S\setminus x$ 不是分离子

引理：任意最小分离子都是一个团

图G的三角剖分是通过给G添加边得到的弦图

图的树宽(tree-width) $treewidth(G)=\{\omega(H)-1: H是G的最小三角剖分\}$ ，其中 $\omega(H)$ 是H的最大团的大小

最大团图(graph of maximal cliques)的顶点是最大团，相交的团之间有边且权重为交集大小

团树定理(clique tree theorem)：弦图的最小生成树是一个宽度为 $\omega(G)-1$ 的树分解(tree decomposition)

图G收缩(contracting)一个边xy后得到图 $G'=(V',E')$ ，$V'=V(G)\setminus \{x,y\}\cup \{z\}$ （z是新顶点）， $E'=E(G[V\setminus\{x,y\}])\cup \{zt: t\in N_G(x)\cup N_G(y)\}$ ($N_G(x)$ 是x的邻居顶点集)

H是G的一个子式(minor)如果H可以通过图G删除顶点，删除边或收缩边得到，子式的树宽小于等于原图的树宽

如果 $treewidth(G)=k$ 那么以G为主图(primal graph)的CSP问题可以在多项式时间内求解（使用k一致性算法）

旅馆预订问题

一个旅馆有k个房间，顾客的订单是三元组 $c_i=(t_i,a_i,d_i)$ ，其中 $t_i$ 是订单创建时间， $a_i$ 是入住时间， $d_i$ 是离开时间。此系统中包含三个实体(entity)：房东，房间，顾客。房间有空闲和被占两种状态。顾客有四种状态：被拒，接收，被分配房间 $r_j$ ，服务结束。房东可触发三种事件(event)：处理请求，接收/拒绝请求，分配房间 $r_j$ 给顾客 $c_i$ 。顾客可触发三种事件：创建订单，到达旅馆，离开旅馆。可能的活动(activity)为顾客 $c_i$ 住在房间 $r_j$ 。每天房东需要根据已经入住的情况和已经接收的订单来决定是否拒绝新订单。考虑三个表： $\sigma_t$ 为在第t天创建的订单列表， $\sigma_A$ 为接收但尚未到达的订单列表， $\sigma_S$ 为已经服务结束的订单列表。对于每个订单 $c_i\in \sigma_t$ ，房东需要使用一个算法来决定是否拒绝订单 $c_i$ ，试探性地分配 $r_i$ 房间给已接收的顾客。

FirstFit算法：

• 输入：房间总数k， $c_i=(a_i,r_i,d_i)\in\sigma_A,\sigma_S,c_i=(t,a_i,d_i)\in\sigma_t$
• 输出：接收/拒绝订单 $c_i$ ，为接收的订单 $c_i$ 分配房间 $r_i$

1. 以非递减的入住时间 $a_i$ 为 $\sigma_t$ 中的订单排序，若存在相等时间，则以非递减的离开时间 $d_i$ 排序。
2. 对 $c_i\in\sigma_t$ ，依次为 $c_i$ 分配在 $[a_i,d_i]$ 内未被占据的最小的房间号 $r_i$ 。若 $r_i\leq k$ 则接收 $c_i$ 并将其添加到 $\sigma_A$ 中，否则拒绝 $c_i$ 并从 $\sigma_t$ 中移除。

BestFit算法：

• 输入：房间总数k， $c_i=(a_i,r_i,d_i)\in\sigma_A,\sigma_S,c_i=(t,a_i,d_i)\in\sigma_t$
• 输出：接收/拒绝订单 $c_i$ ，为接收的订单 $c_i$ 分配房间 $r_i$

1. 以非递减的入住时间 $a_i$ 为 $\sigma_t$ 中的订单排序，若存在相等时间，则分为一组同时处理。
2. 对 $c_i\in\sigma_t$ ，依次为 $c_i$ 分配在 $[a_i,d_i]$ 内未被占据的刚好补上一个空的，或最小的房间号 $r_i$ 。若 $r_i\leq k$ 则接收 $c_i$ 并将其添加到 $\sigma_A$ 中，否则拒绝 $c_i$ 并从 $\sigma_t$ 中移除。

Mealy机

Mealy机是有限自动机的一个变种，它可以在状态转移时打印出字母。Mealy机是一个五元组 $M=(Q,\mathcal V,\Gamma,\delta,q_0)$ ，其中： $Q$ 是状态集， $\mathcal V$ 是输入字母集， $\Gamma$ 是输出字母集， $\delta$ 是转移函数 $\delta:Q\times\mathcal V\to Q\times \Gamma$ ， $q_0$ 是初始状态。在Mealy机中，转移函数是确定性的。

对一个序列反馈电路，状态 $q(t)=I(t) \vee B(t)$ ，新状态由旧状态和输入共同决定： $q(t+1)=(A(t+1),B(t+1))$ ， $A(t+1)=I(t) \barwedge (A(t)\vee B(t))$ ， $B(t+1)=A(t)$ ，对应的Mealy机图为：

向量加法系统(Vector addition systems, VAS)

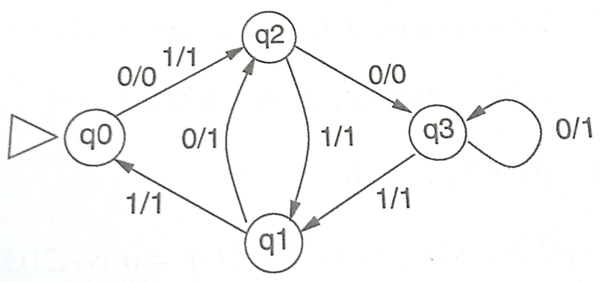
一个VAS是一个有限集合 $U\subseteq \mathbb Z^d, d>0$ 。初始向量编码多个计数器的初始值，VAS中的向量表示更新。通常情况下，这些计数器的值不小于0。给定一个初始向量 $x^0\in \mathbb N^d$ ，向量 $u\in U$ 可以逐项与其做加法，只要保证中间向量 $x^t\in \mathbb N^d$ 。

例：一个系统有4个计数器，VAS $U$ 中有3个向量：

$A=\begin{pmatrix}-1\\-1\\1\\0\end{pmatrix},D=\begin{pmatrix}1\\1\\-1\\0\end{pmatrix},S=\begin{pmatrix}1\\0\\-1\\1\end{pmatrix}$

初始向量 $x=(1,1,0,0)^\top$ ，则有如下状态转换图

Petri网

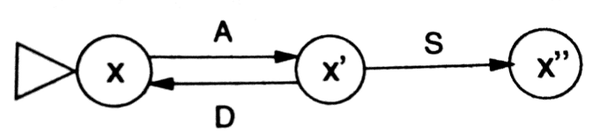
Petri网是一个四元组 $(P,T,f,m_o)$ ，P是地点集，T是转换集， $f:(P\times T)\cup (T\times P)\to \mathbb N_o$ 是流关系，它定义了有向边集，边的权重是非负整数，初始标记是 $m_o:P\to\mathbb N_o$ 。它也是一个加权二分有向图 $G=(P\cup T,A,w)$ ，其中 $P\cup T$ 是节点集，边集 $A$ 包含所有的转换 $pt,tp\subseteq (P\times T)\cup (T\times P)$ ， $f(pt),f(tp)>0$ ，边的权重满足 $w(a)=f(a)$ 。

发射规则(F1)：

• 当 $m(p)\geq f(p,t),\forall p\in \bullet t$ （t之前的地点集）时，转换t在标记m下被激活，记作 $m\ [t>$ ，否则t不被激活。
• 一个被激活的转换t可以发射。
• 当t在m下发射后，一个新的标记m'到达了，记作 $m[t>m'$ ，且有 $m'(p)=m(p)-f(p,t)+f(t,p),\forall p\in P$ 。
• 发射过程不消耗时间

状态空间：

给定一个Petri网$(P,T,f,m_o)$，从初始标记 $m_o$ 可达的标记集合 $[m_o>$ 是它的状态空间

可达图(Reachability graph)：

一个Petri网$(P,T,f,m_o)$的可达图的节点表示从 $m_o$ 可达的标记，边表示导致状态变化的转换的发射

更强的Petri网

在一个Petri网$(P,T,f,m_o)$中，若一些地点有 $B\subseteq P$ 有有限的容量，容量由正整数向量 $\mathbf c\in \mathbb Z_+^B$ ，则将$(P,T,f,m_o,\mathbf c)$称为有容Petri网(cPN)。其中一个转换t在m下被激活，如果

• $\forall p\in \bullet t, m(p)-w(pt)\geq 0$
• $\forall p\in t\bullet \cap B, m(p)+w(pt)\leq c_p$

一个扩展Petri网(xPN) $(P,T,(A\cup A_R\cup A_I),w)$ 有三种边，有正常边 $A$ 和两种控制边：读边 $A_R\subset P\times T$ 和阻碍边 $A_I\subset P\times T$ 。在扩展Petri网中，除了F1发射规则要满足外还要满足：

• $\forall (p,t)\in A_R,m(p)\geq w(pt)$
• $\forall (p,t)\in A_I,m(p)<w(tp)$

一个优先Petri网(pPN)是一个Petri网 $(P,T,f,m_o)$ 加上 $T\times T$ 上的偏序 $\mathcal O$ ，在优先Petri网中，转换的发射被由 $\mathcal O$ 表示的优先级控制。对被激活的转换t，除了F1发射规则要满足外还要满足：

• 不存在转换 $t'\in T(m)$ 且在$\mathcal O$中 $t'>t$

独立系统(Independence system)：对一个有限基础集V，一个集族 $\mathcal V\subseteq 2^V$ 是一个独立系统如果 $\mathcal F$ 满足如下条件：

• $\emptyset\in \mathcal F$
• 若 $F'\subseteq F\in \mathcal F$ ，则$F'\in \mathcal F$

$(V,\mathcal F,c)$ 的最大化问题：对一个独立系统 $(V,\mathcal F)$ 和一个目标函数向量 $\mathbf c\in \mathbb K_+^V$ ，求

$\max \left\{ \mathbf c(F)=\sum_{v\in F} c_v: F\in \mathcal I \right\}$

最大匹配问题(MMP)：给定图 $G=(V,E)$ ，求使 $|M|$ 最大的匹配 $M\subseteq E$ ，或对 $\mathbf w\in \mathbb R^E$ ，使权重 $\mathbf w(M)=\sum_{e\in M} w_e$ 最大的匹配

最大匹配问题是一个独立系统： $\max \left\{ \mathbf w(M)=\sum_{e\in M} w_e: M\in \mathcal M\right\}$

最大匹配问题是一个ILP：

$\max \sum_{e\in E} w_e x_e\\ s.t.\ \sum_{e\in \delta(v)} x_e\leq 1, \forall v\in V\\ x_e\in \{0,1\}, \forall e\in E$

最大稳定集问题(MSSP)：给定图 $G=(V,E)$ ，求使 $|S|$ 最大的稳定集 $S\subseteq V$ ，或对 $\mathbf w\in \mathbb R^E$ ，使权重 $\mathbf w(S)=\sum_{v\in S} w_v$ 最大的稳定集

最大稳定集问题是一个独立系统： $\max \left\{ \mathbf w(S)=\sum_{v\in S} w_v: S\in \mathcal S\right\}$

最大稳定集问题是一个ILP：

$\max \sum_{v\in V} w_v x_v\\ s.t.\ x_u+x_v\leq 1, \forall uv\in E\\ x_v\in \{0,1\}, \forall v\in V$

最小集合划分问题(MSPP)：给定有限基础集V和可行集组成的集族 $\mathcal F\subseteq 2^V$ ，求使 $|\mathcal P|$ 最小的V的划分 $\mathcal P\subseteq \mathcal F$ ，它是一个NP-hard问题

最小集合划分问题是一个ILP：

$\min \sum_{F\in \mathcal F}x_F\\ s.t.\ \sum_{F\ni i}x_F=1, \forall i\in V\\ x_F\in \{0,1\}, \forall F\in \mathcal F$

装箱问题(BPP)：给定基础集 $V=\{1,\cdots,n\}$ ，其中每个货物有权重 $\mathbf a\in \mathbb R_+^n$ ，箱子容量均为 $b\in \mathbb R_+, b\geq a_i,\forall i\in V$ ，求装箱需要的最少箱子数

装箱问题是一个MSPP

节点染色问题(NCP)：给图G=(V,E)染色使相邻节点颜色不同，并使用最少颜色

节点染色问题是一个ILP：

$\min \sum_{S\in \mathcal S}x_S\\ s.t.\ \sum_{S\ni i}x_S=1, \forall i\in V\\ x_S\in \{0,1\}, \forall S\in \mathcal S$

最小集合覆盖问题(MSCP)：给定有限基础集V和可行集组成的集族 $\mathcal F\subseteq 2^V$ ，求使 $|\mathcal C|$ 最小的V的覆盖 $\mathcal C\subseteq \mathcal F$

最小集合覆盖问题是一个ILP：

$\min \sum_{F\in \mathcal F}x_F\\ s.t.\ \sum_{F\ni i}x_F\geq1, \forall i\in V\\ x_F\in \{0,1\}, \forall F\in \mathcal F$

最小截线问题(MTP)：对 $(V,\mathcal F)$ 求基数最小的截线(transversal)。如果 $F',F\in \mathcal F,F'\subset F$ 则对任意截线 $T$ 有$T\cap F'\subset F$ ，因此只需考虑clutter $(V,\mathcal F)$ ，其中没有元素包含在另一个内。

最小截线问题是一个NP-hard问题

clutter矩阵： $M(\mathcal F)$ 由 $F\in\mathcal F$的关联向量作为行向量，是一个0/1矩阵

最小截线问题是一个ILP：

$\min \mathbf 1^\top x\\ s.t.\ M(\mathcal F)x\geq\mathbf 1\\ x\in \{0,1\}^V$

clutter $(V,\mathcal F)$ 可定义一个独立系统 $(V,\mathcal I)$ ， $\mathcal I=\{I\subseteq V:|I\cap F|\leq |F|-1,\forall F\in \mathcal F\}$

反过来一个独立系统 $(V,\mathcal I)$ 的circuits的集族 $\mathcal F=\{F\subseteq V: F\nsubseteq I, \forall I\in \mathcal I, F最小\}$ 可以定义一个clutter $(V,\mathcal F)$

等价关系：对仿射变换 $y=1-x$

$\min \mathbf 1^\top y\\ s.t.\ M(\mathcal F)y\geq\mathbf 1\\ y\in \{0,1\}^V$

和

$|V|-\max\mathbf 1^\top x\\ s.t.\ (x^F)^\top x\leq |F|-1,\forall F\in \mathcal F\\ x\in \{0,1\}^V$

等价。

理想表达式(Ideal formulation)：一个整数线性规划 $\max c^\top x, Ax\leq b, x\in \mathbb Z^n$ 是一个优化问题的理想表达式如果 $P(A,b)=\{x\in\mathbb R_+^n:Ax\leq b\}=conv\{x\in \mathbb Z^n_+:Ax\leq b\}$ ，即 $P(A,b)$ 只有整数极点

全单模(Total unimodualrity)：一个矩阵 $A\in \mathbb Z^{m\times n}$ 是全单模的，如果它的任意方子阵的行列式值属于集合 $\{-1,0,1\}$

定理： $P(A,b)=\{x\in \mathbb R_+^n:Ax\leq b\},\forall b\in \mathbb Z^m$ 是整的，当且仅当A是全单模的

定理：任意有向图的关联矩阵是全单模的

定理：最大流问题对整数容量有整数最优解

定理：最小割问题对整数向量有整数最优解

多边形表达式(Polyhedral formulation)的最大匹配问题：给定G=(V,E)和权重 $w\in \mathbb R_+^E$ ，求 $\max w^\top x, x\in Match(G)$ ，其中 $Match(G)=conv\{x^M\in\{0,1\}^E:M\subseteq E\ matching\}$ 是一个匹配多面体(polytope)。由松弛化得到 度约束多面体(degree constraint polytope)$DegM(G)=\{x\in[0,1]^E :\sum_{e\in\delta(v)}x_e\leq 1,\forall v\in V\}$

定理：矩阵 $M\in \mathbb Z^{m\times n}$ 是全单模的当且仅当任意子集 $J\subset\{1,\cdots,m\}$ 对应的行有二分集 $J_A\cup J_B=J$ ，使得对任意列 $i\in\{1,\dots,n\}$ ，有 $\sum_{j\in J_A} m_{ji}-\sum_{j\in J_B} m_{ji}\in\{-1,0,1\}$

定理：Match(G)=DegM(G)当且仅当G是二分的

定理：对任意图G=(V,E)，匹配多面体Match(G)包含所有满足度约束和奇数集(odd set)约束的 $x\in \mathbb R_+^E$ ，其中

• 度约束： $x(\delta(v))=\sum_{e\in\delta(v)} x_e \leq 1, \forall v\in V$
• 奇数集约束： $x(E(V'))=\sum_{e\in E(V')} x_e\leq \frac{|V'|-1}{2}, \forall V'\in \mathcal O$ 其中 $\mathcal O=\{V'\subseteq V:|V'|\geq 3, odd\}$ 表示奇数大小的节点集族， $E(V')$ 表示端点在V'内的边

因此有松弛化后的最大匹配问题的ILP形式：

$\max \sum_{e\in E} w_e x_e\\ s.t.\ x(\delta(v))=\sum_{e\in\delta(v)} x_e \leq 1, \forall v\in V\\ x(E(V'))=\sum_{e\in E(V')} x_e\leq \frac{|V'|-1}{2}, \forall V'\in \mathcal O\\ x_e\geq 0, \forall e\in E$

结论：存在 $O(\sqrt{|V|}\cdot |E|)$ 的解决最大基数匹配问题的组合算法，和 $O(|V|^3)$ 的解决最大权重匹配问题的组合算法

多边形表达式(Polyhedral formulation)的最大稳定集问题：给定G=(V,E)和权重 $w\in \mathbb R_+^V$ ，求 $\max w^\top x, x\in STAB(G)$ ，其中 $STAB(G)=conv\{x^S\in\{0,1\}^V:S\subseteq V\ stable\}$ 是一个稳定集多面体(polytope)。由松弛化得到 边约束稳定集多面体(edge constraint stable set polytope)$ESTAB(G)=\{x\in[0,1]^V : x_u+x_v\leq 1,\forall uv\in E\}$

定理：矩阵 $M\in \mathbb Z^{m\times n}$ 是全单模的当且仅当任意子集 $I\subset\{1,\cdots,n\}$ 对应的列有二分集 $I_A\cup I_B=I$ ，使得对任意列 $j\in\{1,\dots,m\}$ ，有 $\sum_{i\in I_A} m_{ji}-\sum_{i\in I_B} m_{ji}\in\{-1,0,1\}$

定理：STAB(G)=ESTAB(G)当且仅当G是二分的

定理：一个团Q和一个稳定集S至多有一个公共点

因此有团约束： $x(Q)=\sum_{v\in Q} x_v\leq 1, \forall Q\subseteq V是团$

松弛化后得到团约束稳定集多面体 $QSTAB(G)=\{x\in[0,1]^V :\sum_{v\in Q} x_v\leq 1,\forall Q\subseteq V是团\}$

定理：用 $\omega(G)$ 表示最大团大小， $\chi(G)$ 表示最小染色数，有 $\omega(G)\leq\chi(G)$

完美图：G是完美图当且仅当对G的任意诱导子图 $G'\subseteq G$ 有 $\omega(G')=\chi(G')$

定理：STAB(G)=QSTAB(G)当且仅当G是完美图

定理：对任意完美图，最大稳定集问题可以在多项式时间解决

截线问题的表达式：覆盖多边形(covering polyhedron) $Cov_I(A)=conv\{x\in \{0,1\}^V:Ax\geq \mathbf 1\}$ ，松弛化 $Cov(A)=\{x\in \mathbb R_+^V:Ax\geq \mathbf 1\}$ 是无界的，但是所有极点都在 $[0,1]^V$ 中。

理想cluter：一个clutter $\mathcal C$ 和clutter矩阵 $A=M(\mathcal C)$ 是理想的，如果松弛化Cov(A)有整数极点。阻碍子(blocker) $b(\mathcal C)=(V,\mathcal T)$ 是有 $\mathcal C$ 的最小截线作为超边的clutter

定理：一个clutter $\mathcal C$ 是理想的当且仅当它的阻碍子 $b(\mathcal C)$ 是理想的。Cov(M(C))是理想的当且仅当Cov(M(b(C)))是理想的

定理：有向图D中(s,t)路径的clutter DP(D)是理想的。有向图D中(s,t)割的clutter b(DP(D))是理想的

令 $\mathcal H=(E,\mathcal F)$ 为一个clutter， $\mathcal F $ 中两两不交的集合族是一个packing(matching)。最大packing的基数 $v(\mathcal H)$ 是最小截线的 $\tau(\mathcal H)$ 的下界。当 $v(\mathcal H)=\tau(\mathcal H)$ 时称这个clutter packs，此时对应的线性规划有整数最优解

定理：每个二分图都packs

定理：任意图G=(V,E)中，两两不交(s,t)路径的个数等于最小(s,t)割中的边数。令 $\mathcal P$ 为G中(s,t)路径的集族，超图 $P(G)=(E,\mathcal P)$ packs。

MFMC性质：令 $\mathcal C=(V,\mathcal E)$ 为一个clutter， $A=M(\mathcal C)$ 。若两个等价的线性规划

$\max \mathbf 1^\top y\\ s.t. A^\top y\leq w\\ y\geq 0$ 和

$\min w^\top x\\ Ax\geq \mathbf 1\\ x\geq 0$

对任意 $w\in\mathbb Z_+^V$ 有整数最优解，则 $\mathcal C$ 有MFMC性质

推论：MFMC性质可导出 $\mathcal C$ 是理想的且packs

推论：DP(D)有MFMC性质，b(DP(D))有MFMC性质

综上所述，以下情形下我们可以多项式时间内解决ILP

1. 原来的ILP表达式是理想的，P(A,b)是整的
2. 原表达式不理想，但是松弛化的约束系统容易找到
3. 一般情况下原表达式不理想，但是特殊情形下一些组合性质被满足了

增强表达式的方法：Cutting planes，Branch & Bound

精确和启发式算法：在线算法都是启发式算法

主启发规则(primal heuristic)找到一个可行解I，对偶启发规则找到最优解的下界 $b\leq c(I_{opt})\leq c(I)$

最优间隙(optimality gap)： $c(I)/c(I_{opt})$

对偶间隙(duality gap)： $c(I)/b$

最小化问题的k近似算法找到一个可行解I满足 $c(I)\leq k\cdot c(I_{opt}), k\geq 1$

对一个最小化问题，一个在线算法ALG是c-竞争性的如果ALG对任意请求序列 $\sigma$ 找到一个可行解 $ALG(\sigma)$ 满足 $ALG(\sigma)\leq c\cdot OPT(\sigma), c\geq 1$ ，ALG的竞争性系数(competitive ratio)是保证ALG是c竞争性的所有c的下确界

定理 Olariu1991：当 $\mathcal G(\mathcal I)$ 的节点按左端点升序排序后，贪心算法找到一个区间图(interval graph) $\mathcal G(\mathcal I)$ 的 $\omega(\mathcal G(\mathcal I))$ -染色

定理：旅馆预订问题的在线贪心染色算法是T竞争性的，其中T是总天数

度量任务系统(Metric task system）：一个度量任务系统是一个二元组 $(M,T)$ ，其中 $M=(X,d)$ 是一个度量空间， $T=(\tau_1,\cdots,\tau_n)$ 是任务集合。一个任务 $\tau_i$ 是一个访问特定点 $x_i\in X$ 的请求，或从起点 $x_s\in X$ 到终点 $x_d\in X$ 运输物体的请求。服务器 $server(s)$ 要处理任务集，目标是最小化走过的距离。

TSP是NP-hard问题，有启发规则2-OPT augmentation

定理(Sahni&Gonzalez1976)：设 $H_A$ 为A在 $(K_n,w)$ 中找到的TSP圈。若存在一个多项式的TSP启发规则A和一个常数 $1\leq\alpha<\infty$ 使得对任意TSP实例，有 $w(H_A)\leq \alpha w(H_{opt})$ ，则P=NP

定理(Ausiello 1998)：不存在在线TSP问题的确定性在线算法可以使竞争性系数c<2

定理：在线算法IGNORE和REPLAN在一般度量空间中对在线TSP问题是5/2-竞争性的

定理：存在在线算法在一般度量空间中对在线TSP问题有c=2的竞争性系数

定理(Manasse, McGeoch and Sleator1998)：对任意度量空间，在线kSP的竞争性系数至少为k

定理(Bsaybes, Quilliot, Wagler2018)：出租车问题(紧时间窗口，服务器容量为1的DARP)可以在多项式时间解决

推论：不存在在线PDP(Pickup & delivery)问题的确定性在线算法可以在一般度量空间上使竞争性系数c<2

定理(Ascheuer, Krumke, Rambau1998)：在线算法IGNORE和REPLAN对服务器容量C=1的在线PDP问题是5/2-竞争性的

定理：存在在线算法对服务器容量C=1的在线PDP问题有c=2的竞争性系数

定理(Bsaybes, Quilliot, Wagler2018)：对在线出租车问题，不存在竞争性的在线算法

带重分配的最大接收(Max-Accept Relocation Problem)问题：

• 边a的权重 $w_a$ 即司机沿a移动的消耗，节点v的权重 $c_v$ 即车站的容量。 $x^t\in \mathbb Z^n$ 表示在 $t\in[0,T]$ 时刻每个车站的负载状况
• 输入：由加权图G=(V,E,c,w)诱导的度量空间M=(V,d)和G中的一个计算旅行时间的最短路径度量d。初始状态每个车站 $v\in V$ 的汽车和司机个数 $x_v^0$ 。司机总数k，车队最多汽车数C(可拖车)。顾客预订的请求序列 $\sigma=(r_1,\cdots,r_h)$ ，接收请求 $r_i$ 的利润 $p_i$ 。
• 输出：是否拒绝 $\sigma$ 中的请求，一个重分配汽车的计划
• 目标：最大化利润，最小化重分配汽车的消耗

离线带重分配的最大接收问题对应一个时间展开重分配网络(time-expanded relocation network) $N_{rel}(\sigma)=(V,A)$ ，$V=s^+\cup\{(v,t):v\in V,t\in [0,T]\}\cup s^-$ ， $A=A_+\cup A_P \cup A_\sigma \cup A_L \cup A_-$ ，其中源边(source arc) $(s^+\to (v,0))\in A_+,\forall v\in V$ ，停车边(park arc) $((v,t)\to (v,t+1))\in A_P, \forall v\in V,t\in [0,T)$ ，请求边(request arc) $((v^{pick}_i,t^{pick}_t)\to(v^{drop}_i,t^{drop}_i))\in A_\sigma,\forall r_i\in\sigma$ ， 重分配边(relocation arc)$若 d(v,v')=t'-t, ((v,t)\to(v',t'))\in A_L$ 表示所有重分配车队的移动，漏边(sink arc) $((v,T)\to s^-)\in A_-,\forall v\in V$

因此离线带重分配的最大接收问题被转化为了此网络上汽车流f和司机流F的耦合最大流(coupled flows)问题，得到ILP：

$\max \sum_{a\in A_\sigma} p_a f_a - \sum_{a\in A}w_a F_a\\ s.t.\ \sum_{a\in \delta^+(s^+)} f_a=x^0_v, \sum_{a\in \delta^+(s^+)} F_a=x^0_v\\ \sum_{a\in \delta^-(v,t)} f_a=\sum_{a\in \delta^+(v,t)} f_a,\sum_{a\in \delta^-(v,t)} F_a=\sum_{a\in \delta^+(v,t)} F_a,\forall(v,t)\\ f_a\leq c_v,\forall a\in A_P\\ f_a\leq 1, F_a\leq 0, \forall a\in A_\sigma\\ f_a\leq CF_a,\forall a\in A_L\\ f_a\in \mathbb Z_+,F_a\in\mathbb Z_+,\forall a\in A$

推论：无重分配(relocation)的离线最大接收问题(Max-Accept Problem)可在多项式时间内解决

推论：有重分配的离线最大接收问题是NP-hard问题

定理(KARP1972)：判断一个给定的图G是否有一个使用k个颜色的涂色是NPC问题

定理(Chudnovsky2004)：一个图是完美(perfect)的当且仅当它不包含奇数洞(odd holes) $C_{2k+1}$ 或奇数逆洞(odd antiholes)$\bar C_{2k+1}$， $k\geq 2$ 作为诱导(induced)子图。

引理：对任意图G，有 $\chi(G)\leq\Delta(G)+1$ ，其中 $\Delta(G)$ 是G的最大度数

定理(Brooks1941)：如果G不是一个团(clique)或无弦的奇环路(chordless odd cycle)，则 $\chi(G)\leq \Delta(G)$

区间颜色数(Interval chromatic number)：给定节点加权的图G=(V,E,w)，和一个区间染色 $\mathcal I$，此区间染色的长度(span)定义为 $s(\mathcal I)=\max\{ r(v): v\in V\}-\min\{ l(v): v\in V\}$ 。所有区间染色的最小长度是它的颜色数，记为$\chi_\mathcal I (G,w)$

区间染色问题(Interval coloring problem)：给定节点加权的图G=(V,E,w)，找到一个区间染色(interval coloring) $\mathcal I$ 使长度为 $\chi_\mathcal I (G,w)$

定理(Kubale)：判断一个图是否有一个长度为k的区间染色是NPC问题

加权团数(weighted clique number)：考虑一个加权的图G=(V,E,w)，则加权团数是 $\omega(G,w)=\max\{w(Q):Q\subseteq G\ clique\}\leq\chi_{\mathcal I}(G,w)$ ，它是图G的区间颜色数(chromatic number)的下界

超完美图(super-perfect graph)：若图G=(V,E,w)的任意诱导子图 $G'\subseteq G$ 和任意整数权重w，都有 $\omega(G',w)=\chi_{\mathcal I}(G',w)$

结论：频率分配问题(Frequency allocation problem)是一个特殊的区间染色问题

引理(Marenco, Wagler2007)：频率分配问题存在DegreeGreedy，DemandGreedy，CombinGreedy，RandomGreedy等启发规则和ENUMERATOR的精确解

图 $S$ 和图 $G$ 的子图有哪些同构的问题可以看成一个约束满足问题(CSP) $\mathcal{\langle X,D,C\rangle}$ ，CSP的详细定义见：约束规划，约束传播和CSP问题

子图同构问题的形式化

简单地说，图 $S$ 在 $G$ 中的嵌入（embedding） $f:V(S)\to V(G)$ 满足

(1) $\nexists v_1,v_2\in V(S), v_1\neq v_2,f(v_1)=f(v_2)$ ,

(2) $\forall e=(v_1,v_2)\in E(S), f(e)=(f(v_1),f(v_2))\in E(G)$ ,

(3) $\forall e\notin E(S), f(e)\notin E(G)$ ,

是 $S$ 和 $G$ 的某个子图的同构

标准形式的子图同构问题

$S$ 的每个结点 $v\in V(S)$ 都对应一个变量 $X(v)$ ，因此可以定义双射 $X:V(S)\to \mathcal X$ ，变量集 $\mathcal X=X(V(S))$

每个结点 $v\in V(S)$ 的嵌入一定是 $G$ 中的结点 $u\in V(G)$ ，因此变量$X(v)$ 对应的域为 $D(X(v))=V(G)$ ，域集 $\mathcal D=D(\mathcal X)$

由条件（1）知，有约束条件 $\mathtt{Alldifferent}(X(V(S))$

由条件（2）知，对 $\forall (v_1,v_2)\in E(S)$ ，有约束条件 $\mathtt{AllowedAssignments}((X(v_1),X(v_2)), E(G))$

由条件（3）知，对 $\forall (v_1,v_2)\notin E(S)$ ，有约束条件 $\mathtt{ForbiddenAssignments}((X(v_1),X(v_2)), E(G))$

综合以上3种约束，有约束集 $\mathcal C=\{\mathtt{Alldifferent}(X(V(S))\}\cup \\ \{ \mathtt{AllowedAssignments}((X(v_1),X(v_2)), E(G)): \forall (v_1,v_2)\in E(S)\}\cup \\ \{\mathtt{ForbiddenAssignments}((X(v_1),X(v_2)), E(G)):\forall (v_1,v_2)\notin E(S)\}$

使用求解器求解同构问题

我们已经把子图同构对应的CSP问题$\mathcal{\langle X,D,C\rangle}$表示成了标准形式，因此可以使用求解器进行求解

OR-tools是谷歌开源的运筹学求解器库，详细介绍见：使用谷歌的OR-Tools求解鸡兔同笼

networkx是python的一个图算法库，详细介绍见：python常用代码的第12和13节

以下代码使用OR-tools和networkx求解子图同构问题：

import networkx as nx
from ortools.sat.python import cp_model
from itertools import combinations
def var_from_domain(model, name, domain):
    "initialize a variable with integer domain defined by domain"
    domain = cp_model.Domain.FromIntervals([[i] for i in domain])
    val = model.NewIntVarFromDomain(domain, name)
    return val

# 五角星
G=nx.Graph([(1,3),(1,4),(2,4),(2,5),(3,5)])
# 五边形
S=nx.Graph([(1,2),(2,3),(3,4),(4,5),(5,1)])

model = cp_model.CpModel()

D = list(G.nodes)
X = {i:var_from_domain(model, "X("+str(i)+")", D) for i in S.nodes}

# 约束：嵌入 S -> subgraph of G
model.AddAllDifferent([X[i] for i in S.nodes])
E_G = list(G.edges) + [e[::-1] for e in G.edges]
for v1, v2 in combinations(S.nodes,2):
    if (v1,v2) in S.edges:
        model.AddAllowedAssignments((X[v1],X[v2]), E_G)
    else:
        model.AddForbiddenAssignments((X[v1],X[v2]), E_G)

solver = cp_model.CpSolver()
status = solver.Solve(model)
if status == cp_model.FEASIBLE:
    print("有嵌入:")
    for v, x in X.items():
        print('f(%s)=%i' % (v, solver.Value(x)))
else:
    print("不存在子图同构")

使用openssl生成RSA密钥

openssl genrsa -aes256 -out rsakey.pem 4096

生成的rsakey.pem文件编码的是PEM（Privacy Enhanced Mail）格式的数据。文件的内容使用了ASN.1进行编码，它相当于python的pickle，是一个数据结构的二进制打包，-----BEGIN FOO-----和-----END FOO-----中的FOO是文件的主体，它可能是公钥，密钥或证书。文件的主体是一个DER格式的对象（Distinguished Encoding Rules），使用Base64编码。

使用如下代码读取PEM公钥文件内容：

from Crypto.PublicKey import RSA
with open("public.pem", "rb") as f:
    kobj = RSA.importKey(f.read())
    print(kobj.key.n,kobj.key.e)

使用以下命令来获得十六进制私钥内容：

openssl rsa -in rsakey.pem -noout -text

这些参数与RSA算法中 $p,q,N,e,d$ 的关系如下

N           -> modulus (1024 bit)
e           -> public exponent
d           -> private exponent
p           -> prime1
q           -> prime2
d(mod p-1)  -> exponent1
d(mod q-1)  -> exponent2
q^-1(mod p) -> coefficient

其中后3项是为了使用中国剩余定理来加速解密的

RSA

欧拉统计函数：若 $p,q$ 是素数， $n=pq$ ，则 $\varphi(n)=(p-1)(q-1)$ ， $\varphi(n)$ 也是 $\mathbb Z/n\mathbb Z$ 的所有单位元构成的乘法群的阶，即 $\varphi(n)=|\mathbb Z/n\mathbb Z^\times|$

RSA算法步骤：

1. 密钥生成：随机生成大素数 $p,q$ ，计算$\varphi(n)=(p-1)(q-1)$，随机生成小整数 $e$ （一般固定为0x10001=65537），使用扩展欧几里得算法得到大整数 $d$ 满足 $ed=1 \mod \varphi( n)$
2. 加密：给定明文 $m$ ，加密得到密文 $c=m^e\mod n$
3. 解密：给定密文 $c$ ，解密得到明文 $m = c^d \mod n$

算法解密过程使用了费马-欧拉定理（ $a\bot n \Rightarrow a^{\varphi(n)}=1 \mod n$ ）：

$\begin{align*} c^d\mod n &=m^{ed}\mod n\\ & =m^{1+k\varphi(n)} \mod n\\ &=m \mod n \end{align*}$

RSA算法的使用过程：A使用RSA生成私钥 $d,p,q,\varphi(n)$ ，并把公钥e,n公开；B在获得A的公钥e,n后只能用它来加密，并且B使用A的公钥加密的所有密文只有A可以用自己的私钥解密，其他人包括B都无法解密。注意公钥只用于加密，私钥只用于解密

Cramer-Shoup

算法步骤：

1. 密钥生成：已知一个素数阶的群， $|G|=n$ ，生成元为 $g_1,g_2$，随机生成私钥 $(x_1,x_2,y_1,y_2,z)$，计算公钥 $c=g_1^{x_1}g_2^{x_2},d=g_1^{y_1}g_2^{y_2},h=g_1^z$。
2. 加密：给定明文 $m$ ，随机生成$k$，计算$u_1=g_1^k$，$u_2=g_2^k$，$e=h^km$，计算哈希$\alpha=H(u_1,u_2,e)$，$v=c^kd^{k\alpha}$，得到密文 $(u_1,u_2,e,v)$
3. 解密：计算哈希$\alpha=H(u_1,u_2,e)$，验证$v=u_1^{x_1}u_2^{x_2}(u_1^{y_1}u_1^{y_1})^\alpha$，如果验证通过，则得到明文 $m=\frac{e}{u_1^z}$

计算图如下：
$$\overset{\underline{ \overset{\underline{ x_1 \ x_2 }}{\overset{\downarrow}{c}} } \overset{\underline{ y_1 \ y_2 }}{\overset{\downarrow}{d}} \overset{\underline{ \overset{\underline{ \overset{\underline{ z }}{\overset{\downarrow}{h}} \ m }}{\overset{\downarrow}{e}} \ u_1 \ u_2 }}{\overset{\downarrow}{\alpha}} }{\overset{\downarrow}{v}}$$

Schnorr签名

算法步骤：

1. 密钥生成：已知一个素数阶的群， $|G|=n$ ，生成元为 $g$ ，随机生成签名私钥 $x$ ，生成签名公钥 $y=g^x\mod n$ ，并公开公钥y, g, n
2. 签名生成：已知需要添加签名的明文m，随机生成 $k$ ，得到 $r=g^k \mod n$ ，使用hash函数得到 $e=H(r||m)$ （||表示拼接），使用私钥得到 $s=k-xe$ ，则 $(s,e)$ 就是一个签名
3. 验证签名：已知明文m，签名公钥y, g, n，签名(s,e)，得到 $g^sy^e=r^\prime$ ，计算 $e^\prime=H(r^\prime||m)$ ，若 $e=e^\prime$ 则校验成功，否则失败。

签名的使用过程：网站使用密钥为消息颁发证书并公开公钥，只有网站颁发的证书能通过验证并保证没有被篡改。注意公钥只用于验证签名，私钥只用于生成签名

证书

证书由一个机构的签名公钥，签名算法，本机构信息，颁发证书的父机构信息，过期时间及其他信息构成。不同机构之间互相颁发证书，直至根机构（root CA），构成一个信任链