离散事件模拟
旅馆预订问题
一个旅馆有k个房间,顾客的订单是三元组 $c_i=(t_i,a_i,d_i)$ ,其中 $t_i$ 是订单创建时间, $a_i$ 是入住时间, $d_i$ 是离开时间。此系统中包含三个实体(entity):房东,房间,顾客。房间有空闲和被占两种状态。顾客有四种状态:被拒,接收,被分配房间 $r_j$ ,服务结束。房东可触发三种事件(event):处理请求,接收/拒绝请求,分配房间 $r_j$ 给顾客 $c_i$ 。顾客可触发三种事件:创建订单,到达旅馆,离开旅馆。可能的活动(activity)为顾客 $c_i$ 住在房间 $r_j$ 。每天房东需要根据已经入住的情况和已经接收的订单来决定是否拒绝新订单。考虑三个表: $\sigma_t$ 为在第t天创建的订单列表, $\sigma_A$ 为接收但尚未到达的订单列表, $\sigma_S$ 为已经服务结束的订单列表。对于每个订单 $c_i\in \sigma_t$ ,房东需要使用一个算法来决定是否拒绝订单 $c_i$ ,试探性地分配 $r_i$ 房间给已接收的顾客。
FirstFit算法:
- 输入:房间总数k, $c_i=(a_i,r_i,d_i)\in\sigma_A,\sigma_S,c_i=(t,a_i,d_i)\in\sigma_t$
- 输出:接收/拒绝订单 $c_i$ ,为接收的订单 $c_i$ 分配房间 $r_i$
- 以非递减的入住时间 $a_i$ 为 $\sigma_t$ 中的订单排序,若存在相等时间,则以非递减的离开时间 $d_i$ 排序。
- 对 $c_i\in\sigma_t$ ,依次为 $c_i$ 分配在 $[a_i,d_i]$ 内未被占据的最小的房间号 $r_i$ 。若 $r_i\leq k$ 则接收 $c_i$ 并将其添加到 $\sigma_A$ 中,否则拒绝 $c_i$ 并从 $\sigma_t$ 中移除。
BestFit算法:
- 输入:房间总数k, $c_i=(a_i,r_i,d_i)\in\sigma_A,\sigma_S,c_i=(t,a_i,d_i)\in\sigma_t$
- 输出:接收/拒绝订单 $c_i$ ,为接收的订单 $c_i$ 分配房间 $r_i$
- 以非递减的入住时间 $a_i$ 为 $\sigma_t$ 中的订单排序,若存在相等时间,则分为一组同时处理。
- 对 $c_i\in\sigma_t$ ,依次为 $c_i$ 分配在 $[a_i,d_i]$ 内未被占据的刚好补上一个空的,或最小的房间号 $r_i$ 。若 $r_i\leq k$ 则接收 $c_i$ 并将其添加到 $\sigma_A$ 中,否则拒绝 $c_i$ 并从 $\sigma_t$ 中移除。
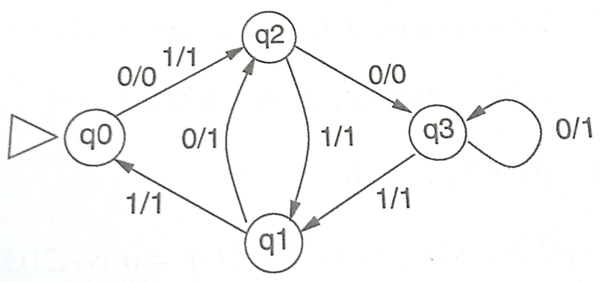
Mealy机
Mealy机是有限自动机的一个变种,它可以在状态转移时打印出字母。Mealy机是一个五元组 $M=(Q,\mathcal V,\Gamma,\delta,q_0)$ ,其中: $Q$ 是状态集, $\mathcal V$ 是输入字母集, $\Gamma$ 是输出字母集, $\delta$ 是转移函数 $\delta:Q\times\mathcal V\to Q\times \Gamma$ , $q_0$ 是初始状态。在Mealy机中,转移函数是确定性的。
对一个序列反馈电路,状态 $q(t)=I(t) \vee B(t)$ ,新状态由旧状态和输入共同决定: $q(t+1)=(A(t+1),B(t+1))$ , $A(t+1)=I(t) \barwedge (A(t)\vee B(t))$ , $B(t+1)=A(t)$ ,对应的Mealy机图为:
向量加法系统(Vector addition systems, VAS)
一个VAS是一个有限集合 $U\subseteq \mathbb Z^d, d>0$ 。初始向量编码多个计数器的初始值,VAS中的向量表示更新。通常情况下,这些计数器的值不小于0。给定一个初始向量 $x^0\in \mathbb N^d$ ,向量 $u\in U$ 可以逐项与其做加法,只要保证中间向量 $x^t\in \mathbb N^d$ 。
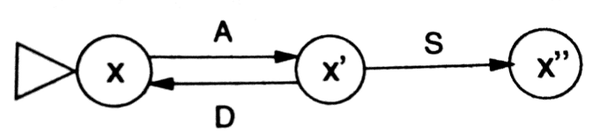
例:一个系统有4个计数器,VAS $U$ 中有3个向量:
$A=\begin{pmatrix}-1\\-1\\1\\0\end{pmatrix},D=\begin{pmatrix}1\\1\\-1\\0\end{pmatrix},S=\begin{pmatrix}1\\0\\-1\\1\end{pmatrix}$
初始向量 $x=(1,1,0,0)^\top$ ,则有如下状态转换图
Petri网
Petri网是一个四元组 $(P,T,f,m_o)$ ,P是地点集,T是转换集, $f:(P\times T)\cup (T\times P)\to \mathbb N_o$ 是流关系,它定义了有向边集,边的权重是非负整数,初始标记是 $m_o:P\to\mathbb N_o$ 。它也是一个加权二分有向图 $G=(P\cup T,A,w)$ ,其中 $P\cup T$ 是节点集,边集 $A$ 包含所有的转换 $pt,tp\subseteq (P\times T)\cup (T\times P)$ , $f(pt),f(tp)>0$ ,边的权重满足 $w(a)=f(a)$ 。
发射规则(F1):
- 当 $m(p)\geq f(p,t),\forall p\in \bullet t$ (t之前的地点集)时,转换t在标记m下被激活,记作 $m\ [t>$ ,否则t不被激活。
- 一个被激活的转换t可以发射。
- 当t在m下发射后,一个新的标记m'到达了,记作 $m[t>m'$ ,且有 $m'(p)=m(p)-f(p,t)+f(t,p),\forall p\in P$ 。
- 发射过程不消耗时间
状态空间:
给定一个Petri网$(P,T,f,m_o)$,从初始标记 $m_o$ 可达的标记集合 $[m_o>$ 是它的状态空间
可达图(Reachability graph):
一个Petri网$(P,T,f,m_o)$的可达图的节点表示从 $m_o$ 可达的标记,边表示导致状态变化的转换的发射
更强的Petri网
在一个Petri网$(P,T,f,m_o)$中,若一些地点有 $B\subseteq P$ 有有限的容量,容量由正整数向量 $\mathbf c\in \mathbb Z_+^B$ ,则将$(P,T,f,m_o,\mathbf c)$称为有容Petri网(cPN)。其中一个转换t在m下被激活,如果
- $\forall p\in \bullet t, m(p)-w(pt)\geq 0$
- $\forall p\in t\bullet \cap B, m(p)+w(pt)\leq c_p$
一个扩展Petri网(xPN) $(P,T,(A\cup A_R\cup A_I),w)$ 有三种边,有正常边 $A$ 和两种控制边:读边 $A_R\subset P\times T$ 和阻碍边 $A_I\subset P\times T$ 。在扩展Petri网中,除了F1发射规则要满足外还要满足:
- $\forall (p,t)\in A_R,m(p)\geq w(pt)$
- $\forall (p,t)\in A_I,m(p)<w(tp)$
一个优先Petri网(pPN)是一个Petri网 $(P,T,f,m_o)$ 加上 $T\times T$ 上的偏序 $\mathcal O$ ,在优先Petri网中,转换的发射被由 $\mathcal O$ 表示的优先级控制。对被激活的转换t,除了F1发射规则要满足外还要满足:
- 不存在转换 $t'\in T(m)$ 且在$\mathcal O$中 $t'>t$
评论已关闭