Haskell初学指南

使用包管理器cabal安装Happy

# 编译安装
cabal get happy && cd happy* && cabal configure && cabal install
# 直接从Hackage安装，--ghc-options="+RTS -M200M" -j1的flag
# 是为了防止并行编译使用过多内存导致内存耗尽，如果内存很大
# 可以去掉。安装Haskell库时要加-lib，用cabal安装二进制程序
# 时不需要加-lib的参数
cabal install happy --ghc-options="+RTS -M200M" -j1

如何在GHCi查看包内的所有函数的签名？

import Data.List
:browse Data.List

import as ?

import qualified Data.Map as Map

如何查看类型，类别（Kinds: types of types），帮助信息？

:t []
:kind Monad
:i Monad

实现两参数函数f的Partial application

elem :: Eq a => a -> t a -> Bool

-- 判断数字是否在列表[1..4]中
isInList :: Int -> Bool
isInList = (`elem` [1..4])

-- 判断4是否在列表中
hasElem :: [Int] -> Bool
hasElem = elem 4

实现Bool类型的异或

{-# LANGUAGE FlexibleInstances #-}
class CanXOR a where
  xor :: a -> a -> a
instance CanXOR [Bool] where
  xor a b = map (\(x,y)->x /= y) (zip a b)
instance CanXOR Bool where
  xor a b = a/=b

列表推导

import Data.List
[(x, y, a) | x <- [1 .. 10], y <- [2..5], even (x+y), let a = 3]
perms [] = [[]]
perms xs = [ x:ps | x <- xs , ps <- perms ( xs\\[x] ) ]

从标准输入中读取整数数组并输出

main = do
    s <- getLine
    let nums = map (\x -> read x::Int) $ words s
    print nums

使用lambda代数实现where

sumSquareOrSquareSum x y = if sumSquare > squareSum
                           then sumSquare
                           else squareSum
    where sumSquare = x^2 + y^2
          squareSum = (x+y)^2
-- 两个函数等价
sumSquareOrSquareSum x y = (\sumSquare squareSum ->
                           if sumSquare > squareSum
                           then sumSquare
                           else squareSum) (x^2 + y^2) ((x+y)^2)

使用lambda代数实现let

overwrite x = let x = 2
              in
               let x = 3
               in
                let x = 4
                in
                 x
-- 两个函数等价
overwrite x = (\x ->
               (\x ->
                (\x -> x) 4
                )3
               )2

使用lambda代数实现变量覆盖（覆盖x）

-- lambda表达式(\x->content)中content里的x会被覆盖
add4 x = (\x->(\x->(\x->x+1) x +1) x +1) x

GCD

gcd a 0 = a
gcd a b = gcd b (mod a b)

实现take

myTake 0 x = []
myTake n [] = []
myTake n (x:xs) = x:(myTake (n-1) xs)

实现drop

myDrop 0 (x:xs) = xs
myDrop n [] = []
myDrop n (x:xs) = x:(myDrop (n-1) xs)

实现reverse

myReverse [] = []
myReverse (x:xs) = (myReverse xs) ++ [x]

两种方法实现Fibonacci数列

--调用栈过深的算法（很慢）
fib 0 = 0
fib 1 = 1
fib n = fib (n-1) + fib (n-2)
--更快的算法
fastFib n1 n2 1 = n2
fastFib n1 n2 counter = fastFib n2 (n1+n2) (counter-1)

实现和filter相反的remove

remove test x = filter (\e->(not (test e))) x

判断是否是回文

isPalindrome x = y == (reverse y) where y= filter (\e->e/=' ') (map toLower x)
-- isPalindrome "A man a plan a canal Panama" -> True

计算调和级数

harmonic n= foldl (\x y->x+1/y) 0 [1..n]

实现对象和类

-- obj类保存一个数字
obj num = \get -> get num

-- 使用getNum方法获取对象保存的数字
getNum ins = ins id

-- subtractByN方法会改变对象的状态
subtractByN ins n = obj ( (getNum ins) - n)

-- 使用isNeg方法检查数据是否小于0
isNeg ins = (getNum ins) < 0

使用Record Syntax 创建新的Robot类型

data Robot = Robot { 
               name :: Name,
               attack :: Attack,
               hp :: HP }

更新名为r的Record中的属性值

setAttack r newAttack = r { attack=newAttack}

实现非Enum类型类的succ函数

cycleSucc :: (Bounded a, Enum a, Eq a) => a -> a
cycleSucc n = if n == maxBound then minBound else succ n

实现骰子类型

data SixSidedDie = S1 | S2 | S3 | S4 | S5 | S6 deriving (Eq,Ord, Enum )
instance Show SixSidedDie where
  show S1 = "one"
  show S2 = "two"
  show S3 = "three"
  show S4 = "four"
  show S5 = "five"
  show S6 = "six"

按元组第2个元素排序

data Name = Name (String, String) deriving (Show, Eq)
instance Ord Name where
    compare (Name (f1,l1)) (Name (f2,l2)) = compare (l1,f1) (l2,f2)

使用Data.Semigroup和guard实现颜色加法幺半群

data Color = Red |
  Yellow |
  Blue |
  Green |
  Purple |
  Orange |
  Brown  |
  Clear deriving (Show,Eq)
instance Semigroup Color where
  (<>) Clear any = any
  (<>) any Clear = any
  (<>) a b | a == b = a
         | all (`elem` [Red,Blue,Purple]) [a,b] = Purple
         | all (`elem` [Blue,Yellow,Green]) [a,b] = Green
         | all (`elem` [Red,Yellow,Orange]) [a,b] = Orange
         | otherwise = Brown
instance Monoid Color where
  mempty = Clear
  mappend = (<>)

从标准输入读取3行并输出

main :: IO ()
main = do
  vals <- mapM (\_ -> getLine) [1..3]
  mapM_ putStrLn vals

从命令行参数接收行数n，从标准输入接收n行数字并求和

-- Filename: sum.hs --
import System.Environment
import Control.Monad
main :: IO ()
main = do
  args <- getArgs
  let linesToRead = if length args > 0
                    then read (head args)
                    else 0 :: Int
  numbers <- replicateM linesToRead getLine
  let ints = map read numbers :: [Int]
  print (sum ints)

-- 使用惰性求值可以更好地处理
-- Filename: sum_lazy.hs
toInts :: String -> [Int]
toInts = map read . lines
main :: IO ()
main = do
  userInput <- getContents
  let numbers = toInts userInput
  print (sum numbers)

Functor，Applicative，和Monad图示

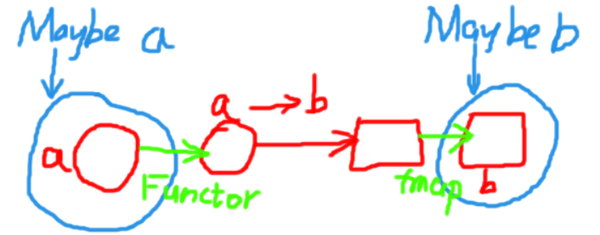
Functor

Functor类型类中最重要的函数是fmap，类型签名是fmap :: (a -> b) -> f a -> f b，如果把f换成Maybe，那么正是上图表示的功能，它可以接受一个a->b的函数和一个在Maybe上下文中的a类型，输出在Maybe上下文中的b类型。

例子：

fmap (+1) (Just 1) -- Output: Just 2
(+1) <$> (Just 1)  -- Output: Just 2
fmap (+1) Nothing  -- Output: Nothing
(+1) <$> Nothing   -- Output: Nothing
show <$> (Just 1)  -- Output: Just "1"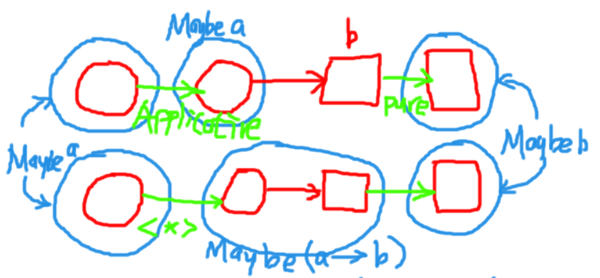

Applicative

Applicative类型类中最重要的函数是pure :: a -> f a和(<*>) :: f (a -> b) -> f a -> f b。

pure可以通过将函数Maybe a -> b和pure:: b -> Maybe b复合，得到Maybe a->Maybe b的函数。

<*>可以接受在Maybe上下文的a和在Maybe上下文中的a->b类型函数（函数可能不存在），输出Maybe上下文中的b。

例子：

sum3 :: Int -> Int -> Int -> Int 
sum3 x y z = x+y+z

-- 这一步只能用fmap(<$>)
sumFunctor :: Maybe (Int -> Int -> Int)
sumFunctor = sum3 <$> (Just 1)

-- 这一步只能用(<*>)
sumApplicative :: Maybe (Int -> Int)
sumApplicative = sumFunctor <*> (Just 2)

-- 总结一下：在Maybe context下对多个参数的pure函数传参可以简单地写成：
sum3 <$> (Just 1) <*> (Just 2) <*> (Just 3)
-- 等价的写法
pure sum3 <*> (Just 1) <*> (Just 2) <*> (Just 3)

-- 列表也是一个context
-- 两个列表中元素两两相加
pure (+) <*> [1..4] <*> [4..7]
-- 笛卡尔积
pure (*) <*> [1..4] <*> [4..7]
-- 构建2元组
pure (,) <*> [1..4] <*> [4..7]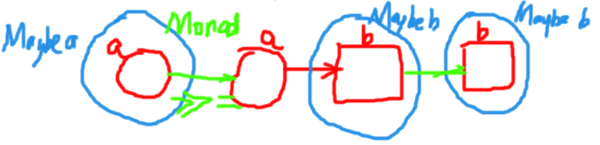

Monad

Monad类型类中最重要的函数是(>>=) :: m a -> (a -> m b) -> m b。此类型签名与上图几乎完全一样，m对应Maybe。

评论已关闭

最新文章

最近回复

分类

归档

其它